Частные производные высших порядков. Частные производные и дифференциалы высших порядков Частные производные высших порядков

1°

1°. Частные производные высших порядков . Частными производными второго порядка функции z=f (х,у) называются частные Производные от ее частных производных первого порядка.

Для производных второго порядка употребляются обозначения

Аналогично определяются и обозначаются частные производные порядка выше второго.

Если частные производные, подлежащие вычислению, непрерывны, то результат многократного дифференцирования не зависит от порядка дифференцирования.

Пример. Найти частные производные второго порядка от функции .

Решение. Найдем сначала частные производные первого порядка:

Теперь дифференцируем вторично:

Заметим, что так называемую «смешанную» частную производную можно найти и иначе, а именно: .

2°. Дифференциалы высших порядков . Дифференциалом второго порядка функции z=f(х, у) называется дифференциал от дифференциала (первого порядка) этой функции d²z=d(dz).

Аналогично определяются дифференциалы функции г порядка выше второго, например: d³z=d(d²z) и, вообще, .

Если z=f(х,у), где х и y - независимые переменные, то дифференциал 2-го порядка функции г вычисляется по формуле

.

Вообще, справедлива символическая формула

,

которая формально развертывается по биномиальному закону.

Если z=f(х,у), где аргументы х и у суть функции одного или нескольких независимых переменных, то

Если х и у - независимые переменные, d ²x =0, d ²y =0 и формула (2) становится тождественной формуле (1).

Пример. Найти полные дифференциалы 1-го и 2-го порядков функции .

а. Мы опять будем говорить лишь о функциях двух переменных (но рассуждения пригодны и для функций любого числа переменных).

Пусть имеем функцию

и - ее частные производные. Последние, очевидно, также являются функциями х и у, а поэтому также можно находить их частные производные по х и по у.

Частная производная по частной производной по называется частной производной второго порядка по и обозначается так:

Аналогично определяем и частную производную второго порядка по у:

Частная производная по у частной производной по называется смешанной второй частной производной по и по у:

Аналогично определяем вторую частную производную, взятую сначала по у, а потом по

Можно доказать, что для многих функций смешанная производная не зависит от порядка дифференцирования, то есть что

Мы не будем приводить (ввиду сложности) доказательства этого важного свойства, а продемонстрируем его на каком-либо примере.

Пусть, например, дана функция

Дифференцируем ее сначала по х, а потом по

Теперь продифференцируем эту функцию сначала по у, а потом по

Как мы видим, результат в обоих случаях получился одинаковым.

Если мы будем брать частные производные по и по у частных производных второго порядка, то получим частные производные третьего порядка

Аналогично определяем частные производные четвертого, пятого порядков и т. д.

b. Подобно тому как мы брали частные производные частных производных, мы можем брать полный дифференциал полного дифференциала. Результат называется вторым полным дифференциалом и обозначается так же, как второй дифференциал функции одной переменной, т. е. так:

Третьим полным дифференциалом называется полный дифференциал второго полного дифференциала и т.

c. Покажем теперь, как выражается второй полный дифференциал через частные производные второго порядка. Для общности мы допустим, что и у могут зависеть от каких-либо других переменных. Обозначим для краткости

Чтобы найти второй полный дифференциал, мы должны взять первый полный дифференциал первого полного дифференциала. Замечая при этом, что, как показано в пункте «е» § 3 этой главы, правило для дифференцирования суммы и произведения применимо и к полному дифференциалу, мы можем написать

Так как p и q сами являются функциями двух переменных х и у, то

Заметим, что

Подставляя их в последнюю формулу, после раскрытия скобок окончательно получим

Если х и у являются независимыми переменными или линейными функциями других каких-либо переменных, то их вторые дифференциалы равны нулю;

и формула (8) упрощается:

Мы видим, что закон инвариантности применим ко второму дифференциалу лишь с очень большими ограничениями: он будет верен только в том случае, если х и у являются линейными функциями других переменных, во всех остальных случаях он неприменим. Рассматривая формулу (9), мы видим, что она очень напоминает формулу квадрата суммы двух чисел. Эта аналогия навела на мысль записывать второй дифференциал в нижеследующей символической форме:

Порядка n , где n > 1 , от функции z {\displaystyle z} в некоторой точке называется дифференциал в этой точке от дифференциала порядка (n - 1) , то есть

d n z = d (d n − 1 z) {\displaystyle d^{n}z=d(d^{n-1}z)} .

Энциклопедичный YouTube

  • 1 / 5

    Для функции, зависящей от одной независимой переменной второй и третий дифференциалы выглядят так:

    d 2 z = d (d z) = d (z ′ d x) = d z ′ d x = (z ″ d x) d x = z ″ d x 2 {\displaystyle d^{2}z=d(dz)=d(z"dx)=dz"dx=(z""dx)dx=z""dx^{2}} , d 3 z = d (d 2 z) = d (z ″ d x 2) = d z ″ d x 2 = (z ‴ d x) d x 2 = z ‴ d x 3 {\displaystyle d^{3}z=d(d^{2}z)=d(z""dx^{2})=dz""dx^{2}=(z"""dx)dx^{2}=z"""dx^{3}} .

    Отсюда можно вывести общий вид дифференциала n -го порядка от функции z = f (x) {\displaystyle z=f(x)} , при условии, что x {\displaystyle x} - независимая переменная:

    d n z = z (n) d x n {\displaystyle d^{n}z=z^{(n)}dx^{n}} .

    При вычислении дифференциалов высших порядков очень важно, что d x {\displaystyle dx} есть произвольное и не зависящее от x {\displaystyle x} , которое при дифференцировании по x {\displaystyle x} следует рассматривать как постоянный множитель. Если x {\displaystyle x} не является независимой переменной, то дифференциал будет другим (см. ) .

    Дифференциал высшего порядка функции нескольких переменных

    Если функция z = f (x , y) {\displaystyle z=f(x,y)} имеет непрерывные частные производные второго порядка, то дифференциал второго порядка определяется так: d 2 z = d (d z) {\displaystyle d^{2}z=d(dz)} .

    d 2 z = d (∂ z ∂ x d x + ∂ z ∂ y d y) = (∂ z ∂ x d x + ∂ z ∂ y d y) x ′ d x + (∂ z ∂ x d x + ∂ z ∂ y d y) y ′ d y = {\displaystyle d^{2}z=d\left({\frac {\partial z}{\partial x}}dx+{\frac {\partial z}{\partial y}}dy\right)=\left({\frac {\partial z}{\partial x}}dx+{\frac {\partial z}{\partial y}}dy\right)"_{x}dx+\left({\frac {\partial z}{\partial x}}dx+{\frac {\partial z}{\partial y}}dy\right)"_{y}dy=} = (∂ 2 z ∂ x 2 d x + ∂ 2 z ∂ y ∂ x d y) d x + (∂ 2 z ∂ x ∂ y d x + ∂ 2 z ∂ y 2 d y) d y {\displaystyle =\left({\frac {\partial ^{2}z}{\partial x^{2}}}dx+{\frac {\partial ^{2}z}{\partial y\partial x}}dy\right)dx+\left({\frac {\partial ^{2}z}{\partial x\partial y}}dx+{\frac {\partial ^{2}z}{\partial y^{2}}}dy\right)dy} d 2 z = ∂ 2 z ∂ x 2 d x 2 + 2 ∂ 2 z ∂ x ∂ y d x d y + ∂ 2 z ∂ y 2 d y 2 {\displaystyle d^{2}z={\frac {\partial ^{2}z}{\partial x^{2}}}dx^{2}+2{\frac {\partial ^{2}z}{\partial x\partial y}}dxdy+{\frac {\partial ^{2}z}{\partial y^{2}}}dy^{2}} d 2 z = (∂ ∂ x d x + ∂ ∂ y d y) 2 z {\displaystyle d^{2}z=\left({\frac {\partial }{\partial x}}dx+{\frac {\partial }{\partial y}}dy\right)^{2}z}

    Символически общий вид дифференциала n -го порядка от функции z = f (x 1 , . . . , x r) {\displaystyle z=f(x_{1},...,x_{r})} выглядит следующим образом:

    d n z = (∂ ∂ x 1 d x 1 + ∂ ∂ x 2 d x 2 + . . . + ∂ ∂ x r d x r) n z {\displaystyle d^{n}z=\left({\frac {\partial }{\partial x_{1}}}dx_{1}+{\frac {\partial }{\partial x_{2}}}dx_{2}+...+{\frac {\partial }{\partial x_{r}}}dx_{r}\right)^{n}z}

    где z = f (x 1 , x 2 , . . . x r) {\displaystyle z=f(x_{1},x_{2},...x_{r})} , а произвольные приращения независимых переменных x 1 , . . . , x r {\displaystyle x_{1},...,x_{r}} .
    Приращения d x 1 , . . . , d x r {\displaystyle dx_{1},...,dx_{r}} рассматриваются как постоянные и остаются одними и теми же при переходе от одного дифференциала к следующему. Сложность выражения дифференциала возрастает с увеличением числа переменных.

    Неинвариантность дифференциалов высшего порядка

    При n ⩾ 2 {\displaystyle n\geqslant 2} n {\displaystyle n} -й дифференциал не инвариантен (в отличие от инвариантности первого дифференциала), то есть выражение d n f {\displaystyle d^{n}f} зависит, вообще говоря, от того, рассматривается ли переменная x {\displaystyle x} как независимая, либо как некоторая промежуточная функция другого переменного, например, x = φ (t) {\displaystyle x=\varphi (t)} .

    Так, для независимой переменной x {\displaystyle x} второй дифференциал, как было сказано выше, имеет вид:

    d 2 z = z ″ (d x) 2 {\displaystyle d^{2}z=z""(dx)^{2}}

    Если же переменная x {\displaystyle x} сама может зависеть от других переменных, то d (d x) = d 2 x ≠ 0 {\displaystyle d(dx)=d^{2}x\neq 0} . В этом случае формула для второго дифференциала будет иметь вид :

    d 2 z = d (d z) = d (z ′ d x) = z ″ (d x) 2 + z ′ d 2 x {\displaystyle d^{2}z=d(dz)=d(z"dx)=z""\,(dx)^{2}+z"d^{2}x} .

    Аналогично, третий дифференциал примет вид:

    d 3 z = z ‴ (d x) 3 + 3 z ″ d x d 2 x + z ′ d 3 x {\displaystyle d^{3}z=z"""\,(dx)^{3}+3z""dx\,d^{2}x+z"d^{3}x} .

    Для доказательства неинвариантности дифференциалов высшего порядка достаточно привести пример.
    При n = 2 {\displaystyle n=2} и y = f (x) = x 3 {\displaystyle y=f(x)=x^{3}} :

    С учётом зависимости x = t 2 {\displaystyle x=t^{2}} , уже второй дифференциал не обладает свойством инвариантности при замене переменной. Также не инвариантны дифференциалы порядков 3 и выше.

    Дополнения

    • для функции с одной переменной:
    4 F (x 0) = d F (x 0) + d 2 F (x 0) 2 ! + . . . + d n F (x 0) n ! + d n + 1 F (x 0 + θ 4 x) (n + 1) ! {\displaystyle {\mathcal {4}}F(x_{0})=dF(x_{0})+{\frac {d^{2}F(x_{0})}{2!}}+...+{\frac {d^{n}F(x_{0})}{n!}}+{\frac {d^{n+1}F(x_{0}+\theta {\mathcal {4}}x)}{(n+1)!}}} , (0 < θ < 1) {\displaystyle (0<\theta <1)} ;
    • для функции с несколькими переменными:
    4 F (x 0 , y 0) = d F (x 0 , y 0) + d 2 F (x 0 , y 0) 2 ! + . . . + d n F (x 0 , y 0) n ! + d n + 1 F (x 0 + θ 4 x , y 0 + θ 4 y) (n + 1) ! {\displaystyle {\mathcal {4}}F(x_{0},y_{0})=dF(x_{0},y_{0})+{\frac {d^{2}F(x_{0},y_{0})}{2!}}+...+{\frac {d^{n}F(x_{0},y_{0})}{n!}}+{\frac {d^{n+1}F(x_{0}+\theta {\mathcal {4}}x,y_{0}+\theta {\mathcal {4}}y)}{(n+1)!}}} , (0 < θ < 1) {\displaystyle (0<\theta <1)}

    Пусть задана функция двух переменных. Дадим аргументу приращение, а аргумент оставим неизменным. Тогда функция получит приращение, которое называется частным приращением по переменной и обозначается:

    Аналогично, фиксируя аргумент и придавая аргументу прираще-ние, получим частное приращение функции по переменной:

    Величина называется полным прира-щениием функции в точке.

    Определение 4. Частной производной функции двух переменных по одной из этих переменных называется предел отношения соответствующего частного приращения функции к приращению данной переменной, когда последнее стремится к нулю (если этот предел существует). Обозначается частная производная так: или, или.

    Таким образом, по определению имеем:

    Частные производные функции вычисляются по тем же правилам и формулам, что и функция одной переменной, при этом учитывается, что при дифференцировании по переменной, считается постоянной, а при дифференцировании по переменной постоянной считается.

    Пример 3. Найти частные производные функций:

    Решение. а) Чтобы найти считаем постоянной величиной и дифференцируем как функцию одной переменной:

    Аналогично, считая постоянной величиной, находим:

    Определение 5. Полным дифференциалом функции называется сумма произведений частных производных этой функции на приращения соответствующих независимых переменных, т.е.

    Учитывая, что дифференциалы независимых переменных совпадают с их приращениями, т.е. , формулу полного дифференциала можно записать в виде

    Пример 4. Найти полный дифференциал функции.

    Решение. Так как, то по формуле полного дифференциала находим

    Частные производные высших порядков

    Частные производные и называют частными производными первого порядка или первыми частными производными.

    Определение 6. Частными производными второго порядка функции называются частные производные от частных производных первого порядка.

    Частных производных второго порядка четыре. Они обозначаются следующим образом:

    Аналогично определяются частные производные 3-го, 4-го и более высоких порядков. Например, для функции имеем:

    Частные производные второго или более высокого порядка, взятые по различным переменным, называются смешанными частными производными. Для функции таковыми являются производные. Заметим, что в случае, когда смешанные производные непрерывны, то имеет место равенство.

    Пример 5. Найти частные производные второго порядка функции

    Решение. Частные производные первого порядка для данной функции найдены в примере 3:

    Дифференцируя и по переменным х и y, получим

    Каждая частная производная (по x и по y ) функции двух переменных представляет собой обыкновенную производную функции одной переменной при фиксированном значении другой переменной:

    (где y = const),

    (где x = const).

    Поэтому частные производные вычисляют по формулам и правилам вычисления производных функций одной переменной , считая при этом другую переменную постоянной (константой).

    Если Вам не нужен разбор примеров и необходимого для этого минимума теории, а нужно лишь решение Вашей задачи, то переходите к калькулятору частных производных онлайн .

    Если тяжело сосредоточиться, чтобы отслеживать, где в функции константа, то можно в черновом решении примера вместо переменной с фиксированным значением подставить любое число - тогда можно будет быстрее вычислить частную производную как обыкновенную производную функции одной переменной. Надо только не забыть при чистовом оформлении вернуть на место константу (переменную с фиксированном значением).

    Описанное выше свойство частных производных следует из определения частной производной, которое может попасться в экзаменационных вопросах. Поэтому для ознакомления с определением ниже можно открыть теоретическую справку.

    Понятие непрерывности функции z = f (x , y ) в точке определяется аналогично этому понятию для функции одной переменной.

    Функция z = f (x , y ) называется непрерывной в точке если

    Разность (2) называется полным приращением функции z (оно получается в результате приращений обоих аргументов).

    Пусть заданы функция z = f (x , y ) и точка

    Если изменение функции z происходит при изменении только одного из аргументов, например, x , при фиксированном значении другого аргумента y , то функция получит приращение

    называемое частным приращением функции f (x , y ) по x .

    Рассматривая изменение функции z в зависимости от изменения только одного из аргументов, мы фактически переходим к функции одной переменной.

    Если существует конечный предел

    то он называется частной производной функции f (x , y ) по аргументу x и обозначается одним из символов

    (4)

    Аналогично определяются частное приращение z по y :

    и частная производная f (x , y ) по y :

    (6)

    Пример 1.

    Решение. Находим частную производную по переменной "икс":

    (y фиксировано);

    Находим частную производную по переменной "игрек":

    (x фиксировано).

    Как видно, не имеет значения, в какой степени переменная, которая фиксирована: в данном случае это просто некоторое число, являющееся множителем (как в случае обычной производной) при переменной, по которой находим частную производную. Если же фиксированная переменная не умножена на переменную, по которой находим частную производную, то эта одинокая константа, безразлично, в какой степени, как и в случае обычной производной, обращается в нуль.

    Пример 2. Дана функция

    Найти частные производные

    (по иксу) и (по игреку) и вычислить их значения в точке А (1; 2).

    Решение. При фиксированном y производная первого слагаемого находится как производная степенной функции (таблица производных функций одной переменной ):

    .

    При фиксированном x производная первого слагаемого находится как производная показательной функции, а второго – как производная постоянной:

    Теперь вычислим значения этих частных производных в точке А (1; 2):

    Проверить решение задач с частными производными можно на калькуляторе частных производных онлайн .

    Пример 3. Найти частные производные функции

    Решение. В один шаг находим

    (y x , как если бы аргументом синуса было 5x : точно так же 5 оказывается перед знаком функции);

    (x фиксировано и является в данном случае множителем при y ).

    Проверить решение задач с частными производными можно на калькуляторе частных производных онлайн .

    Аналогично определяются частные производные функции трёх и более переменных.

    Если каждому набору значений (x ; y ; ...; t ) независимых переменных из множества D соответствует одно определённое значение u из множества E , то u называют функцией переменных x , y , ..., t и обозначают u = f (x , y , ..., t ).

    Для функций трёх и более переменных геометрической интерпретации не существует.

    Частные производные функции нескольких переменных определяются и вычисляются также в предположении, что меняется только одна из независимых переменных, а другие при этом фиксированы.

    Пример 4. Найти частные производные функции

    .

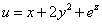    Решение. y и z фиксированы:

    x и z фиксированы:

    x и y фиксированы:

    Найти частные производные самостоятельно, а затем посмотреть решения

    Пример 5.

    Пример 6. Найти частные производные функции .

    Частная производная функции нескольких переменных имеет тот же механический смысл, что и производная функции одной переменной , - это скорость изменения функции относительно изменения одного из аргументов.

    Пример 8. Количественная величина потока П пассажиров железных дорог может быть выражена функцией

    где П – количество пассажиров, N – число жителей корреспондирующих пунктов, R – расстоянии между пунктами.

    Частная производная функции П по R , равная

    показывает, что уменьшение потока пассажиров обратно пропорционально квадрату расстояния между корреспондирующими пунктами при одной и той же численности жителей в пунктах.

    Частная производная П по N , равная

    показывает, что увеличение потока пассажиров пропорционально удвоенному числу жителей населённых пунктов при одном и том же расстоянии между пунктами.

    Проверить решение задач с частными производными можно на калькуляторе частных производных онлайн .

    Полный дифференциал

    Произведение частной производной на приращение соответствующей независимой переменной называется частным дифференциалом. Частные дифференциалы обозначаются так:

    Сумма частных дифференциалов по всем независимым переменным даёт полный дифференциал. Для функции двух независимых переменных полный дифференциал выражается равенством

    (7)

    Пример 9. Найти полный дифференциал функции

    Решение. Результат использования формулы (7):

    Функция, имеющая полный дифференциал в каждой точке некоторой области, называется дифференцируемой в этой области.

    Найти полный дифференциал самостоятельно, а затем посмотреть решение

    Так же как и в случае функции одной переменной, из дифференцируемости функции в некоторой области следует её непрерывность в этой области, но не наоборот.

    Сформулируем без доказательств достаточное условие дифференцируемости функции.

    Теорема. Если функция z = f (x , y ) имеет непрерывные частные производные

    в данной области, то она дифференцируема в этой области и её дифференциал выражается формулой (7).

    Можно показать, что подобно тому, как в случае функции одной переменной дифференциал функции является главной линейной частью приращения функции , так и в случае функции нескольких переменных полный дифференциал является главной, линейной относительно приращений независимых переменных частью полного приращения функции.

    Для функции двух переменных полное приращение функции имеет вид

    (8)

    где α и β – бесконечно малые при и .

    Частные производные высших порядков

    Частные производные и функции f (x , y ) сами являются некоторыми функциями тех же переменных и, в свою очередь, могут иметь производные по разным переменным, которые называются частными производными высших порядков.