Введем понятие еще об одной основной динамической характеристике движения о кинетической энергии. Кинетической энергией материальной точки называется скалярная величина равная половине произведения массы точки на квадрат ее скорости.
Единица измерения кинетической энергии та же, что и работы (в СИ - 1 Дж). Найдем зависимость, которой связаны эти две величины.
Рассмотрим материальную точку с массой , перемещающуюся из положения , где она имеет скорость в положение , где ее скорость
Для получения искомой зависимости обратимся к выражающему основной закон динамики уравнению Проектируя обе его части на касательную к траектории точки М, направленную в сторону движения, получим
![]()
Входящее сюда касательное ускорение точки представим в виде
![]()
В результате найдем, что
![]()
Умножим обе части этого равенства на и внесем под знак дифференциала. Тогда, замечая, что где - элементарная работа силы получим выражение теоремы об изменении кинетической энергии точки в дифференциальной форме:
![]()
Проинтегрировав теперь обе части этого равенства в пределах, соответствующих значениям переменных в точках найдем окончательно
![]()
Уравнение (52) выражает теорему об изменении кинетической энергии точки в конечном виде: изменение кинетической энергии точки при некотором ее перемещении равно алгебраической сумме работ всех действующих на точку сил на том же перемещении.
Случай несвободного движения. При несвободном движении точки в правую часть равенства (52) войдет работа заданных (активных) сил и работа реакции связи. Ограничимся рассмотрением движения точки по неподвижной гладкой (лишенной трения) поверхности или кривой. В этом случае реакция N (см. рис. 233) будет направлена по нормали к траектории точки и . Тогда, согласно формуле (44), работа реакции неподвижной гладкой поверхности (или кривой) при любом перемещении точки будет равна нулю, и из уравнения (52) получим
![]()
Следовательно, при перемещении по неподвижной гладкой поверхности (или кривой) изменение кинетической энергии точки равно сумме работ на этом перемещении приложенных к точке активных сил.
Если поверхность (кривая) не является гладкой, то к работе активных сил прибавится работа силы трения (см. § 88). Если же поверхность (кривая) движется, то абсолютное перемещение точки М может не быть перпендикулярно N и тогда работа реакции N не будет равна нулю (например, работа реакции платформы лифта).
Решение задач. Теорема об изменении кинетической энергии [формула (52)] позволяет, зная как при движении точки изменяется ее скорость, определить работу действующих сил (первая задача динамики) или, зная работу действующих сил, определить, как изменяется при движении скорость точки (вторая задача динамики). При решении второй задачи, когда заданы силы, надо вычислить их работу. Как видно из формул (44), (44), это можно сделать лишь тогда, когда силы постоянны или зависят только от положения (координат) движущейся точки, как, например, силы упругости или тяготения (см. § 88).
Таким образом, формулу (52) можно непосредственно использовать для решения второй задачи динамики, когда в задаче в число данных и искомых величин входят: действующие силы, перемещение точки и ее начальная и конечная скорости (т. е. величины ), причем силы должны быть постоянными или зависящими только от положения (координат) точки.
Теорему в дифференциальной форме [формула (51)] можно, конечно, применять при любых действующих силах.

Задача 98. Груз массой кг, брошенный со скоростью из пункта А, находящегося на высоте (рис. 235), имеет в точке падения С скорость Определить, чему равна работа действующей на груз при его движении силы сопротивления воздуха
Решение. На груз при его движении действуют сила тяжести Р и сила сопротивления воздуха R. По теореме об изменении кинетической энергии, считая груз материальной точкой, имеем
Из этого равенства, так как согласно формуле находим
Задача 99. При условиях задачи 96 (см.[§ 84) определить, какой путь пройдет груз до остановки (см. рис, 223, где - начальное положение груза, а - конечное).
Решение. На груз, как и в задаче 96, действуют силы Р, N, F. Для определения тормозного пути учитывая, что в условия данной задачи входят и постоянная сила F, воспользуемся теоремой об изменении кинетической энергии
В рассматриваемом случае - скорость груза в момент остановки). Кроме того, так как силы Р и N перпендикулярны перемещению, В итоге получаем откуда находим
По результатам задачи 96 время торможения растет пропорционально начальной скорости, а тормозной путь, как мы нашли, - пропорционально квадрату начальной скорости. Применительно к наземному транспорту это показывает, как возрастает опасность с увеличением скорости движения.
Задача 100. Груз весом Р подвешен на нити длиной l Нить вместе с грузом отклоняют от вертикали на угол (рис. 236, а) и отпускают без начальной скорости. При движении на груз действует сила сопротивления R, которую приближенно заменяем ее средним значением Найти скорость груза в тот момент времени, когда нить образует с вертикалью угол
Решение. Учитывая условия задачи, воспользуемся опять теоремой (52):
На груз действуют сила тяжести Р, реакция нити сопротивления, представленная ее средним значением R. Для силы Р по формуле (47) для силы N, так как получим наконец, для силы так как по формуле (45) будет (длина s дуги равна произведению радиуса l на центральный угол ). Кроме того, по условиям задачи В результате равенство (а) дает:
При отсутствии сопротивления получаем отсюда известную формулу Галилея справедливую, очевидно, и для скорости свободно падающего груза (рис, 236, б).

В рассматриваемой задаче Тогда, введя еще обозначение - средняя сила сопротивления, приходящаяся на единицу веса груза), получаем окончательно
Задача 101. Пружина клапана имеет в недеформироваином состоянии длину см. При полностью открытом клапане ее длина см, а высота подъема клапана см (рис. 237). Жесткость пружины масса клапана кг. Пренебрегая действием силы тяжести и сил сопротивления, определить скорость клапана в момент его закрытая.
Решение, Воспользуемся уравнением
По условиям задачи работу совершает только сила упругости пружины. Тогда по формуле (48) будет
В данном случае
Кроме того, Подставляя все эти значения в уравнение (а), получим окончательно
![]()
Задача 102. Груз, лежащий на середине упругой балки (рис. 238), прогибает ее на величину (статистический прогиб балки) Пренебрегая весом балки, определить, чему будет равен ее максимальный прогиб если груз упадет на балку с высоты Н.
Решение. Как и в предыдущей задаче, воспользуемся для решения уравнением (52). В данном случае начальная скорость груза и конечная его скорость (В момент максимального прогиба балки) равны нулю и уравнение (52) принимает вид
Работу здесь совершают сила тяжести Р на перемещении и сила упругости балки F на перемещении При этом так как для балкн Подставляя эти величины в равенство (а), получим
Но при равновесии груза на балке сила тяжести уравновешивается силой упругости, следовательно, и предыдущее равенство можно представить в виде
Решая это квадратное уравнение и учитывая, что по условиям задачи должно быть находим
Интересно отметить, что при получается Следовательно, если груз положить на середину горизонтальной балки, то ее максимальный прогиб при опускании груза будет равен удвоенному статическому. В дальнейшем груз начнет вместе с балкой совершать колебания около равновесного положения. Под влиянием сопротивлений эти колебания затухнут и система уравновесится в положении, при котором прогиб балки равен


Задача 103. Определить, наименьшую направленную вертикально виерх начальную скорость надо сообщить телу, чтобы оно поднялось с поверхности Земли на заданную высоту Н (рис 239) Силу притяжения считать изменяющейся обратно пропорционально квадрату расстояния от центра Земли. Сопротивлением воздуха пренебречь.
Решение. Рассматривая тело как материальную точку с массой , воспользуемся уравнением
Работу здесь совершает сила тяготения F. Тогда по формуле (50), учитывая, что в данном случае где R - радиус Земли, получим
Так как в наивысшей точке то при найденном значении работы уравнение (а) дает
![]()
Рассмотрим частные случай:
а) пусть Н очень мало по сравнению с R. Тогда - величина, близкая к нулю. Деля числитель и знаменатель получим
![]()
Таким образом, при малых Н приходим к формуле Галилея;
б) найдем, при какой начальной скорости брошенное тело уйдет в бесконечность, Деля числитель и знаменатель на А, получим
Если рассмотреть какую-нибудь точку системы с массой , имеющую скорость , то для этой точки будет
![]() ,
,
где и - элементарные работы действующих на точку внешних и внутренних сил. Составляя такие уравнения для каждой из точек системы и складывая их почленно, получим
![]() ,
,
![]() . (2)
. (2)
Равенство выражает теорему об изменении кинетической энергии системы в дифференциальной форме.
Если полученное выражение отнести к элементарному промежутку времени, в течение которого произошло рассматриваемое перемещение, можно получить вторую формулировку для дифференциальной формы теоремы: производная по времени от кинетической энергии механической системы равна сумме мощностей всех внешних () и внутренних () сил, т.е.
Дифференциальными формами теоремы об изменении кинетической энергии можно воспользоваться для составления дифференциальных уравнений движения, но это делается достаточно редко, потому что есть более удобные приемы.
Проинтегрировав обе части равенства (2) в пределах, соответствующих перемещению системы из некоторого начального положения, где кинетическая энергия равна , в положение, где значение кинетической энергии становится равным , будемиметь
Полученное уравнение выражает теорему об изменении кинетической энергии в конечном виде: изменение кинетической энергии системы при некотором ее перемещении равно сумме работ на этом перемещении всех приложенных к системе внешних и внутренних сил.
В отличие от предыдущих теорем, внутренние силы в уравнениях не исключаются. В самом деле, если и - силы взаимодействия между точками и системы (см. рис.51), то . Но при этом точка , может перемещаться по направлению к , а точка - по направлению к . Работа каждой из сил будет тогда положительной и сумма работ нулем не будет. Примером может служить явление отката. Внутренние силы (силы давления), действующие и на снаряд и на откатывающиеся части, совершают здесь положительную работу. Сумма этих работ, не равная нулю, и изменяет кинетическую энергию системы от величины в начале выстрела до величины конце.
Другой пример: две точки, соединенные пружиной. При изменении расстояния между точками упругие силы, приложенные к точкам, будут совершать работу. Но если система состоит из абсолютно твердых тел и связи между ними неизменяемые, не упругие, идеальные, то работа внутренних сил будет равна нулю и их можно не учитывать и вообще не показывать на расчетной схеме.
Рассмотрим два важных частных случая.
1) Неизменяемая система . Неизменяемой будем называть систему, в которой расстояния между точками приложения внутренних сил при движении системы не изменяются. В частности, такой системой является абсолютно твердое тело или нерастяжимая нить.

Рис.51
Пусть две точки и неизменяемой системы (pис.51), действующие друг на друга с силами и () имеют в данный момент скорости и . Тогда за промежуток времени dt эти точки совершат элементарные перемещения и , направленные вдоль векторов и . Но таккак отрезок является неизменяемым, то по известной теореме кинематики проекции векторов и , а, следовательно, и перемещений и на направление отрезка будут равны друг другу, т.е. . Тогда элементарные работы сил и будут одинаковы по модулю и противоположны по знаку и в сумме дадут нуль. Этот результат справедлив для всех внутренних сил при любом перемещении системы.
Отсюда заключаем, что для неизменяемой системы сумма работ всех внутренних сил равна нулю и уравнения принимают вид
2) Система с идеальными связями . Рассмотрим систему, на которую наложены связи, не изменяющиеся со временем. Разделим все действующие на точки системы внешние и внутренние силы на активные и реакции связей. Тогда
![]() ,
,
где - элементарная работа действующих на k- ю точку системы внешних и внутренних активных сил, a - элементарная работа реакций наложенных на ту же точку внешних и внутренних связей.
Как видим, изменение кинетической энергии системы зависит от работы и активных сил и реакций связей. Однако можно ввести понятие о таких «идеальных» механических системах, у которых наличие связей не влияет на изменение кинетической энергии системы при ее движении. Для таких связей должно, очевидно, выполняться условие:
Если для связей, не изменяющихся со временем, сумма работ всех реакций при элементарном перемещении системы равна нулю, то такие связи называют идеальными. Для механической системы, на которую наложены только не изменяющиеся со временем идеальные связи, будем, очевидно, иметь
Таким образом, изменение кинетической энергии системы с идеальными, не изменяющимися со временем связями при любом ее перемещении равно сумме работ на этом перемещении, приложенных к системе внешних и внутренних активных сил.
Механическая система называется консервативной (энергия ее как бы законсервирована, не изменяется), если для нее имеет место интеграл энергии
![]() или (3)
или (3)
Это есть закон сохранения механической энергии: при движении системы в потенциальном поле механическая энергия ее (сумма потенциальной и кинетической) все время остается неизменной, постоянной.
Механическая система будет консервативной, если действующие на нее силы потенциальны, например сила тяжести, силы упругости. В консервативных механических системах с помощью интеграла энергии можно проводить проверку правильности составления дифференциальных уравнений движения. Если система консервативна, а условие (3) не выполняется, значит при составлении уравнений движения допущена ошибка.
Интегралом энергии можно воспользоваться для проверки правильности составления уравнений и другим способом, без вычисления производной. Для этого следует после проведения численного интегрирования уравнений движения вычислить значение полной механической энергии для двух различных моментов времени, например, начального и конечного. Если разница значений окажется сопоставимой с погрешностями вычислений, это будет свидетельствовать о правильности используемых уравнений.
Все предыдущие теоремы позволяли исключить из уравнений движения внутренние силы, но все внешние силы, в том числе и наперед неизвестные реакции внешних связей, в уравнениях сохранялись. Практическая ценность теоремы об изменении кинетической энергии состоит в том, что при не изменяющихся со временем идеальных связях она позволит исключить из уравнений движения все наперед неизвестные реакции связей.
Данная теорема устанавливает количественную взаимосвязь между работой силы (причиной) и кинетической энергией материальной точки (следствием).
Кинетической энергией материальной точки называется скалярная величина, равная половине произведения массы точки на квадрат ее скорости
 .
(43)
.
(43)
Кинетическая энергия характеризует то механическое действие силы, которое может превратиться в другие виды энергии, например, в тепловую.
Работой силы на данном перемещении называется характеристика того действия силы, которое приводит к изменению модуля скорости.
Элементарная работа силы определяется как скалярное произведение вектора силы на элементарный вектор перемещения в точке ее приложения

 ,
(44)
,
(44)
где
 -
элементарное перемещение.
-
элементарное перемещение.
Модуль элементарной работы определяется формулой
где
- угол между вектором силы и вектором
элементарного перемещения;
 -
проекция вектора силы на касательную.
-
проекция вектора силы на касательную.
Полная работа на некотором конечном перемещении определяется интегралом
 .
(46)
.
(46)
Из (46) следует, что полная работа может быть вычислена в двух случаях, когда сила постоянная или зависит то перемещения.
При
F
=const
получаем
 .
.
При решении задач часто удобно пользоваться аналитическим способом вычисления силы
где F x , F y , F z – проекции силы на координатные оси.
Докажем следующую теорему.
Теорема : Изменение кинетической энергии материальной точки на некотором ее перемещении равно работе силы, действующей на точку, на том же перемещении.
Пусть материальная точка M массы m движется под действием силы F из положения M 0 в положение M 1 .
ОУД:
 .
(47)
.
(47)
Введем
подстановку
 и спроектируем (47)
на касательную
и спроектируем (47)
на касательную
 .
(48)
.
(48)
Разделяем в (48) переменные и интегрируем

В результате получим
 .
(49)
.
(49)
Уравнение (49) доказывает сформулированную выше теорему.
Теоремой удобно пользоваться, когда среди заданных и искомых параметров присутствуют масса точки, ее начальная и конечная скорость, силы и перемещение.
Вычисление работы характерных сил.
1. Работа силы тяжести вычисляется как произведение модуля силы на перемещение точки ее приложения по вертикали
 .
(50)
.
(50)
При перемещении вверх работа положительная, при перемещении вниз – отрицательная.
2. Работа упругой силы пружины F =-cx равна
 ,
(51)
,
(51)
где x 0 – начальное удлинение (сжатие) пружины;
x 1 – конечное удлинение (сжатие) пружины.
Работа силы тяжести и упругой силы не зависят от траектории перемещения их точек приложения. Такие силы, работа которых не зависит от траектории, называются потенциальными силами .
3. Работа силы трения .
Так как сила трения всегда направлена в сторону, противоположную направлению перемещения, то ее работа равна
Работа силы трения всегда отрицательная . Силы работа которых всегда отрицательна, называются диссипативными .
Кинетической энергией материальной точки k называется скалярная величина, равная половине произведения массы точки на квадрат ее скорости . Кинетической энергией механической системы называется арифметическая сумма кинетических энергий всех точек системы
![]() . (3.35)
. (3.35)
Найдем формулы для вычисления кинетической энергии тел в разных случаях движения.
Поступательное движение . В этом случае скорости всех точек тела одинаковы , где скорость центра масс тела.
Вращательное движение . Скорость –ой точки тела , где расстояние точки до оси вращения.
![]() , (3.37)
, (3.37)
где момент инерции тела относительно оси вращения .
Плоское движение . Из кинематики известно, что плоское движение в некоторый момент времени можно рассматривать как мгновенный поворот тела вокруг оси, проходящей через мгновенный центр скоростей.
В этом случае . Пусть точка – центр масс. По теореме Гюйгенса-Штейнера (3.22): ![]() . Кинетическая энергия тела при плоском движении
. Кинетическая энергия тела при плоском движении

![]()
![]() . (3.38)
. (3.38)
Здесь момент инерции тела относительно центральной оси, скорость центра масс, мгновенная угловая скорость, – масса тела.
Докажем теорему об изменении кинетической энергии для материальной точки . Запишем второй закон Ньютона в проекции на касательную (3.5): .
Касательное ускорение![]() или
или  , (3.39)
, (3.39)
где элементарная работа силы на перемещении точки . Элементарную работу можно записать иначе:
 · . (3.40)
· . (3.40)
Здесь · скалярное произведение векторов, ![]() радиус-вектор точки .
радиус-вектор точки .
Поскольку , то аналитическое выражение элементарной работы силы :
Проинтегрировав (3.39) в пределах изменения переменных в точках и , найдем окончательно
![]() . (3.42)
. (3.42)
Это уравнение выражает теорему об изменении кинетической энергии материальной точки в интегральной форме: изменение кинетической энергии точки на некотором ее перемещении равно сумме работ приложенных сил на том же перемещении.
Для произвольной точки механической системы выражение(3.42) имеет вид: ![]() . Для всей системы
. Для всей системы ![]() . Если обозначить кинетическую энергию всей системы в ее начальном положении
. Если обозначить кинетическую энергию всей системы в ее начальном положении
А в конечном положении , то
![]() . (3.43)
. (3.43)
Уравнение (3.43) выражает теорему об изменении кинетической энергии механической системы в интегральной форме: изменение кинетической энергии системы при некотором ее перемещении равно сумме работ на этом перемещении всех приложенных к системе внешних и внутренних сил. Отметим, что в общем случае сумма работ внутренних сил не равна нулю. Для абсолютно твердого тела , так как расстояния между любыми точками тела не изменяются.
Работа силы тяжести
. Пусть точка переместилась под действием силы тяжести из положения в положение (рис. 3.7). По формуле (3.41) найдем элементарную работу силы : Полная работа силы на перемещении будет ![]() или
или
 |
где − высота, на которую опустилась точка. Таким образом, работа силы тяжести положительна, когда точка опускается, и отрицательна, когда точка поднимается.
Работа силы упругости пружины
. Пусть груз прикреплен к пружине жесткости с
(рис. 3.8). Выберем начало координаты в положении , при котором пружина не деформирована (ее длина равна l
), и определим работу силы упругости пружины при перемещении ее нижнего конца из начального положения в конечное положение . Пусть λ , λ начальная и конечная деформации пружины. Согласно закону Гука . Проекции силы на оси координат: . Элементарная работа ![]() . Полная работа
. Полная работа
– λ –λ )или = (λ –λ ). (3.45)
Работа силы упругости положительна, если начальная λ деформация пружины больше конечной λ .
Работа силы трения скольжения . Пусть тело перемещается по наклонной шероховатой плоскости из положения в положение . Действующая на тело сила трения , где – нормальная реакция плоскости, – коэффициент трения скольжения. Сила трения направлена противоположно перемещению тела, поэтому работа силы трения отрицательна. Если считать силу трения во время движения постоянной, то. Нетрудно заметить, что – момент силы относительно оси вращения . Будем называть величину вращающим моментом . Тогда элементарная работа . При повороте на конечный угол работа
 , (3.47)
, (3.47)
а в случае постоянного момента из (3.47) следует .
Вопросы для самоконтроля
Просмотр: эта статья прочитана 49915 раз
Pdf Выберите язык... Русский Украинский Английский
Краткий обзор
Полностью материал скачивается выше, предварительно выбрав язык
Два случая преобразования механического движения материальной точки или системы точек:
- механическое движение переносится с одной механической системы на другую в качестве механического движения;
- механическое движение превращается в другую форму движения материи (в форму потенциальной энергии, теплоту, электричество и т.д.).
Когда рассматривается преобразование механического движения без перехода его в другую форму движения, мерой механического движения является вектор количества движения материальной точки или механической системы. Мерой действия силы в этом случае является вектор импульса силы.
Когда механическое движение превращается в другую форму движения материи, в качестве меры механического движения выступает кинетическая энергия материальной точки или механической системы. Мерой действия силы при превращении механического движения в другую форму движения является работа силы
Кинетическая энергия
Кинетическая энергия это способность тела преодолевать препятствование во время движения.
Кинетическая энергия материальной точки
Кинетической энергией материальной точки называется скалярная величина, которая равняется половине произведения массы точки на квадрат ее скорости.
Кинетическая энергия:
- характеризует и поступательное, и вращательное движения;
- не зависит от направления движения точек системы и не характеризует изменение этих направлений;
- характеризует действие и внутренних, и внешних сил.
Кинетическая энергия механической системы
Кинетическая энергия системы равняется сумме кинетических энергий тел системы. Кинетическая энергия зависит от вида движения тел системы.
Определение кинетической энергии твердого тела при разных видах движения движениях.
Кинетическая энергия поступательного движения
При поступательном движении кинетическая энергия тела равна Т
=m
V 2 /2.
Мерой инертности тела при поступательном движении является масса.
Кинетическая энергия вращательного движения тела
При вращательном движении тела кинетическая энергия равняется половине произведения момента инерции тела относительно оси вращения и квадрата его угловой скорости.
Мерой инертности тела при вращательном движении является момент инерции.
Кинетическая энергия тела не зависит от направления вращения тела.
Кинетическая энергия плоскопаралельного движения тела
При плоскопаралельном движении тела кинетическая энергия равна
Работа силы
Работа силы характеризует действие силы на тело при некотором перемещении и определяет изменение модуля скорости подвижной точки.
Элементарная работа силы
Элементарная работа силы определяется как скалярная величина, равная произведению проекции силы на касательную к траектории, направленную в направлении движения точки, и бесконечно малого перемещения точки, направленного вдоль этой касательной.
Работа силы на конечном перемещении
Работа силы на конечном перемещении равна сумме ее работ на элементарных участках.
Работа силы на конечном перемещении М 1 М 0 равняется интегралу вдоль этого перемещения от элементарной работы.
Работа силы на перемещении М 1 М 2 изображается площадью фигуры, ограниченной осью абсцисс, кривой и ординатами, соответствующими точкам М 1 и М 0 .
Единица измерения работы силы и кинетической энергии в системе СИ 1 (Дж).
Теоремы о работе силы
Теорема 1 . Работа равнодействующей силы на некотором перемещении равна алгебраической сумме работ составляющих сил на том же перемещении.
Теорема 2. Работа постоянной силы на результирующем перемещении равна алгебраической сумме работ этой силы на составляющих перемещениях.
Мощность
Мощность - это величина, которая определяет работу силы за единицу времени.
Единицей измерения мощности есть 1Вт = 1 Дж/с.
Случаи определения работы сил
Работа внутренних сил
Сумма работ внутренних сил твердого тела на любом его перемещении равна нулю.
Работа силы тяжести
Работа силы упругости
Работа силы трения
Работа сил, приложенных к вращающемуся телу
Элементарная работа сил, приложенных к твердому телу, вращающемуся вокруг неподвижной оси, равна произведению главного момента внешних сил относительно оси вращения на приращение угла поворота.
Сопротивление качению
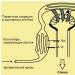
В зоне контакта неподвижого цилиндра и плоскости возникает местная деформация контактного сжатия, напряжение распределяются по эллиптическому закону и линия действия равнодействующей N этих напряжений совпадает с линией действия силы нагрузки на цилиндр Q. При перекатывании цилиндра распределение нагрузки становится несимметричным с максимумом, смещенным в сторону движения. Равнодействующая N смещается на величину k - плечо силы трения качения, которая еще назвается коэффициентом трения качения и имеет размерность длины (см)
Теорема об изменении кинетической энергии материальной точки
Изменение кинетической энергии материальной точки на некотором ее перемещении равняется алгебраической сумме робот всех действующих на точку сил на том же перемещении.
Теорема об изменении кинетической энергии механической системы
Изменение кинетической энергии механической системы на некотором перемещении равняется алгебраической сумме робот внутренних и внешних сил, действующих на материальные точки системы на том же перемещении.
Теорема об изменении кинетической энергии твердого тела
Изменение кинетической энергии твердого тела (неизменной системы) на некотором перемещении равняется сумме робот внешних сил, действующих на точки системы на том же перемещении.
КПД
Силы, действующие в механизмах
Силы и пары сил (моменты), которые приложены к механизму или машине, можно разделить на группы:
1.Движущие силы и моменты, совершающие положительную работу (приложенные к ведущим звеньям, например, давление газа на поршень в ДВС).
2. Силы и моменты сопротивления, совершающие отрицательную работу:
- полезного сопротивления (совершают требуемую от машины работу и приложены к ведомым звеньям, например сопротивление поднимаемого машиной груза),
- силы сопротивления (например, силы трения, сопротивление воздуха и т.п.).
3. Силы тяжести и силы упругости пружин (как положительная, так и отрицательная работа, при этом работа за полный цикл равна нулю).
4. Силы и моменты, приложенные к корпусу или стойке извне (реакция фундамента и т.п.), которые не совершают работу.
5. Силы взаимодействия между звеньями, действующие в кинематических парах.
6. Силы инерции звеньев, обусловленные массой и движением звеньев с ускорением, могут осуществлять положительную, отрицательную работу и не совершать работы.
Работа сил в механизмах
При установившемся режиме работы машины ее кинетическая энергия не изменяется и сумма работ приложенных к ней движущих сил и сил сопротивления равна нулю.
Работа, затрачиваемая на приведение машины в движение, расходуется на преодоление полезных и вредных сопротивлений.
КПД механизмов
Механический коэффициент полезного действия при установившемся движении равен отношению полезной работы машины к работе, затраченной на приведение машины в движение:
Элементы машины могут соединяться последовательно, параллельно и смешанно.
КПД при последовательном соединении
При последовательном соединении механизмов общий КПД меньше с наименьшего КПД отдельного механизма.
КПД при параллельном соединении
При параллельном соединении механизмов общий КПД больше наименьшего и меньше наибольшего КПД отдельного механизма.
Формат: pdf
Язык: русский, украинский
Пример расчета прямозубой цилиндрической передачи
Пример расчета прямозубой цилиндрической передачи. Выполнен выбор материала, расчет допускаемых напряжений, расчет на контактную и изгибную прочность.
Пример решения задачи на изгиб балки
В примере построены эпюры поперечных сил и изгибающих моментов, найдено опасное сечение и подобран двутавр. В задаче проанализировано построение эпюр с помощью дифференциальных зависимостей, провелен сравнительный анализ различных поперечных сечений балки.
Пример решения задачи на кручение вала
Задача состоит в проверке прочности стального вала при заданном диаметре, материале и допускаемых напряжениях. В ходе решения строятся эпюры крутящих моментов, касательных напряжений и углов закручивания. Собственный вес вала не учитывается
Пример решения задачи на растяжение-сжатие стержня
Задача состоит в проверке прочности стального стержня при заданных допускаемых напряжениях. В ходе решения строятся эпюры продольных сил, нормальных напряжений и перемещений. Собственный вес стержня не учитывается
Применение теоремы о сохранении кинетической энергии
Пример решения задачи на применение теоремы о сохранение кинетической энергии механической системы