7.1 Сущность и задачи стохастического моделирования
Задачи детерминированного факторного анализа (ДФА) нашли широкое применение в практике аналитической работы, однако детерминированный подход не позволяет учитывать влияние на результативный показатель очень многих факторов, не находящихся с ним в пропорциональной зависимости (спрос, текучесть кадров, размещение торговой сети и т. д.). Кроме того, в задачах ДФА невозможно выделить результаты одновременно действующих факторов. Эти недостатки обусловили необходимость применения стохастического моделирования в экономическом анализе, называемого иначе математико-статистическими методами изучения связей, которые являются в определенной степени дополнением и углублением ДФА.
Таким образом, в экономическом анализе стохастические модели используются в тех случаях, когда необходимо:
– оценить влияние факторов, по которым нельзя построить жестко детерминированную модель;
– изучить и сравнить влияние факторов, которые нельзя включить в одну и ту же детерминированную модель;
– выделить и оценить влияние сложных факторов, которые не могут быть выражены одним определенным количественным показателем.
В отличие от детерминированного, стохастический подход для своей реализации требует выполнения ряда предпосылок:
1. Качественная однородность совокупности, т. е. в пределах варьирования значений факторов не должно происходить качественного скачка в характере отражаемого явления.
2. Достаточная численность совокупности наблюдения, позволяющая с точностью и надежностью выявить имеющиеся закономерности (в теории статистики считается, что количество наблюдений должно в 6-8 раз превышать количество факторов).
3. Наличие методов, т. е. специального математического аппарата, позволяющего выявить тесноту связи между изучаемыми показателями и оценить величину влияния факторов на изменение результативного показателя.
В целом стохастическое моделирование предназначено для решения трех задач:
1) установление факта наличия или отсутствия связи между изучаемыми признаками;
2) выявление причинных связей между изучаемыми показателями и количественное измерение действия факторов на результативный показатель;
3) прогнозирование неизвестных значений результативных показателей.
Проведение стохастического моделирования осуществляется согласно следующим этапам:
1) качественный анализ, подразумевающий постановку цели анализа, определение результативных и факторных признаков, отбор и отсев факторов;
2) количественный анализ, т. е. построение регрессионной модели (уравнения регрессии) и расчет параметров уравнений регрессии;
3) проверка адекватности модели, т. е. оценка точности (надежности) уравнения связи и правомерности его использования для практической цели.
Практическая реализация указанных этапов основывается на применении корреляционного и регрессионного методов анализа, рассмотренных ниже.
7.2 Методы стохастического моделирования
Методы стохастического моделирования включают в себя корреляционно-регрессионный анализ, в результате которого будут рассчитаны коэффициенты ее тесноты и значимости (т. е. проведен корреляционный анализ); будет построена регрессионная зависимость (т.е. проведен регрессионный анализ), позволяющая количественно измерить действия факторов на результативный показатель.
1. Корреляционный метод позволяет количественно выразить взаимосвязь между показателями. При этом если показатель зависит от одного фактора, то речь идет о парной корреляции, если он зависит от множества факторов, то о множественной корреляции. Основная особенность корреляционного анализа в том, что он устанавливает лишь факт наличия связи и степень ее тесноты, не вскрывая причины.
Задача корреляционного анализа – выявить тесноту связи изучаемых признаков, что осуществляется либо с помощью коэффициента корреляции (при прямолинейной зависимости), либо с помощью корреляционного отношения (при линейной и нелинейной зависимости).
Коэффициент корреляции (парный коэффициент корреляции, линейный коэффициент корреляции) между фактором х и результативным показателем Y определяется следующим образом:
где y – абсолютное значение результативного показателя; x – абсолютное значение фактора; n – количество наблюдений.
Коэффициент корреляции может принимать значения от –1 до +1. При этом если:
r = -1, то это означает наличие функциональной связи обратно-пропорционального характера;
r = +1, то это означает наличие функциональной связи прямо-пропорционального характера (и в этом и в другом случае переходят к детерминированному факторному анализу);
r = 0, то это означает отсутствие связи между фактором и изучаемым результативным показателем (фактор исключается из факторной системы);
Другие значения r свидетельствуют о наличии стохастической зависимости, причем чем больше /r/ стремится к 1, тем связь теснее. В частности:
/r/ < 0,3 означает слабую связь;
0,3 < /r/ < 0,7 – связь средней тесноты;
/r/ > 0,7 – связь тесная, т. е. имеется объективная возможность перейти к стохастическому факторному анализу.
При парной корреляции теснота связи изучается между результативным признаком и фактором.
В случае множественной корреляции тесноту связи между результативным показателем и набором факторов изучают на основе коэффициента множественной корреляции (R):
 ,
,
где – среднее значение результативного показателя, вычисленное по уравнению регрессии; – среднее значение результативного показателя, вычисленное по исходным данным.
Коэффициент множественной корреляции принимает только положительные значения в пределах от 0 до 1. При значении R≤0,3 говорят о малой зависимости между величинами, при значении 0,3 < R< 0,6 – о средней тесноте связи, при R>0,6 – о наличии существенной связи.
При множественной корреляции теснота связи изучается:
– между результативным признаком (функцией) и каждой переменной (аргументом);
– между переменными попарно.
Альтернативным показателем степени зависимости между двумя переменными является коэффициент детерминации, представляющий собой возведение в квадрат коэффициента корреляции (r 2 или R 2 – величина достоверности аппроксимации). Коэффициент детерминации, значение которого должно стремиться к 1, показывает, чему равна доля влияния изучаемого (изучаемых) фактора (факторов) на результативный показатель. При этом следует помнить, что при условии, если r 2 (или R 2)<0,5, синтезированные математические модели связи практического значения не имеют.
Практическая реализация корреляционного анализа включает следующие последовательные этапы:
1) постановка задач и выбор признаков;
2) формирование массива исходной статистической информации, определение степени ее однородности (на основе коэффициента вариации);
3) предварительная характеристика взаимосвязи (аналитические группировки, графики);
4) устранение мультиколлинеарности (взаимозависимости факторов), уточнение набора факторов (отбор наиболее существенных) на основе коэффициента корреляции, индекса детерминации или критерия Стьюдента (подробно см. п. 7.3). При этом в ходе отбора факторов следует придерживаться следующих правил:
– учитывать причинно-следственные связи между показателями (не рекомендуется включать в модель взаимосвязанные факторы: если парный коэффициент корреляции между двумя факторами больше 0,85, то один из них необходимо исключить).
– отбирать самые значимые факторы;
– рассматривать только те факторы, которые должны быть количественно измеримы, т. е. иметь единицу измерения и находить отражение в учете и отчетности;
– учитывать только однонаправленные факторы (т. е. при линейном характере зависимости нельзя включать в модель факторы, связь которых с результативным показателем имеет криволинейный характер);
После осуществления всех вышеуказанных процедур в случае установления факта высокой тесноты связи (> 0,7) приступают к решению второй задачи – регрессионному анализу, который позволяет выявить конкретные величины влияния факторов на изменение результативного показателя.
2. Регрессионный анализ – это метод установления аналитического выражения (т.е. уравнения регрессии) стохастической зависимости между исследуемыми признаками.
Уравнение регрессии показывает, как в среднем изменяется результативный признак (Y) при изменении любой из переменных (Х i) и имеет вид: Y = f (x 1 ,x 2,… x n),
где Y – зависимая переменная, т.е. результативный показатель; x i – независимые переменные (факторы).
В ходе регрессионного анализа решаются две главные задачи:
– построение уравнения регрессии, т. е. нахождение вида зависимости между результативным показателем и независимыми факторами;
– оценка значимости полученного уравнения (на основе коэффициента детерминации, критерия Фишера и критерия Стьюдента).
Вид уравнения регрессии определяется по графику, изображающему связь между факторами и результативным показателем, который строится на основе однородной совокупности статистических данных и служит обоснованием уравнения связи.
Если зависимость линейная (на графике изображена в виде прямой восходящей или снисходящей линии), то при:
а) однофакторном анализе уравнение будет иметь вид: Y(х) = а +b·x,
где Y – результативный показатель; b – коэффициент регрессии, который показывает, насколько изменится результативный показатель при изменении фактора на 1 ед.; а – свободный член, который показывает величину влияния неучтенных факторов; х – фактор;
б) многофакторном анализе уравнение будет иметь вид:
Y(х) = а +b 1 x 1 + b 2 x 2 +…+ b n x n.
Если зависимость нелинейная (на графике изображена в виде параболы или гиперболы), то уравнение регрессии принимает следующий вид:
Y(х) = а +b·x + с·x 2 – при графике в виде параболы;
Y(х) = а +b:x 2 – при графике в виде гиперболы.
При сложном характере зависимости между изучаемыми явлениями используются более сложные параболы (третьего, четвертого порядка (полинома) и т. д.), а также квадратическое, степенные, показательные и другие функции.
Выбор конкретного уравнения регрессии и его решение осуществляется в рамках табличного процессора MS Excel или статистического программного пакета STADIA.
Сущность решения уравнений регрессии заключается в нахождении параметров регрессии (а и b). Это осуществляется по способу наименьших квадратов с использованием системы нормальных уравнений, суть которого заключается в минимизации суммы квадратов отклонений фактических значений результативного показателя от его расчетных значений.
При прямолинейной зависимости система нормальных уравнений имеет вид:
∑y = na +b∑x
∑xy = a∑x +b∑x 2 .
При криволинейной зависимости:
∑y(1/x)= a∑1/x +b∑(1/x) 2 .
Для оценки адекватности модели используют такие критерии, как ошибка аппроксимации, F-отношения, коэффициента детерминации, подробно рассмотренные в п. 7.3.
В необходимых случаях построение уравнения регрессии может быть использовано для прогнозирования результативного признака.
Апробируем методику корреляционно-регрессионного анализа на конкретном примере.
Пример 7.1 На основании данных табл. А необходимо проанализировать зависимость между расходами на оплату труда (Y) и выручкой от продажи товаров (х).
Таблица А – Данные о выручке от продажи товаров и сумме расходов на оплату труда в разрезе торговых организаций тыс. руб.
| № мага-зинов | Выручка от продажи товаров | № магазинов | Выручка от продажи товаров | Сумма расходов на оплату труда | |
| А | 1 | 2 | Б | 3 | 4 |
| 1. | 3 200 | 190 | 15. | 1 690 | 177 |
| 2. | 500 | 45 | 16. | 7 450 | 230 |
| 3. | 12 000 | 670 | 17. | 12 900 | 587 |
| 4. | 8 560 | 345 | 18. | 2 010 | 166 |
| 5. | 14 100 | 713 | 19. | 1 650 | 105 |
| 6. | 11 300 | 470 | 20. | 5 115 | 241 |
| 7. | 4 300 | 194 | 21. | 8 945 | 400 |
| 8. | 1 010 | 98 | 22. | 11 900 | 523 |
| 9. | 8 230 | 244 | 23. | 14 200 | 780 |
| 10. | 12 560 | 510 | 24. | 10 300 | 576 |
| 11. | 6 201 | 215 | 25. | 11 450 | 425 |
| 12. | 11 500 | 603 | 26. | 13 000 | 606 |
| 13. | 13 300 | 575 | 27. | 6 100 | 210 |
| 14. | 1 000 | 95 | 28. | 7 500 | 249 |
На основании данных табл. А построим график зависимости изменения расходов на оплату труда от изменения товарооборота (см. рисунок).

Зависимость динамики расходов на оплату труда от выручки от продажи товаров
Данные графика свидетельствуют о том, что между расходами на оплату труда и выручкой от продажи товаров существует прямолинейная зависимость. Далее измерим тесноту связи между изучаемыми показателями на основе коэффициента корреляции, для чего сгруппируем магазины по сумме выручки от продажи товаров (см. тему 3) и составим следующую разработочную таблицу (табл. Б).
Таблица Б – Разработочная таблица для определения показателей, используемых при расчете коэффициента корреляции
| Группы магазинов по сумме выручки от продажи товаров | Количество магазинов | Выручка от продажи товаров (x i), млн руб. | Сумма расходов на оплату труда (y i), млн руб. | |||
| От 500 до 3 220 включ. | 7,000 | 11,060 | 0,876 | 9,689 | 122,324 | 0,768 |
| От 3 221 до 5 440 включ. | 2,000 | 9,415 | 0,435 | 4,096 | 88,642 | 0,190 |
| От 5 441 до 8 160 включ. | 4,000 | 27,251 | 0,904 | 24,635 | 742,617 | 0,818 |
| От 8 161 до 10 880 включ. | 4,000 | 36,035 | 1,565 | 56,394 | 1298,521 | 2,450 |
| Св. 10 881 | 11,000 | 138,210 | 5,859 | 809,772 | 19102,004 | 34,328 |
| Итого | 28,000 | 221,971 | 9,639 | 904,586 | 21354,107 | 38,550 |
Примечание. Согласно данным таблицы, элементы расчета коэффициента корреляции имеют следующие значения:
Σx i = 221,971;
Σy i = 9,639; Σy i x i =904,586; Σx 2 i = 21 354,107; Σy 2 = 38,550.
Рассчитанные данные подставляются в формулу коэффициента корреляции:
r = 
Коэффициент детерминации: r 2 =0,8 2 =0,64.
Коэффициент корреляции, равный 0,8 ед., означает наличие высокой стохастической зависимости между суммой расходов на оплату труда и выручкой от реализации. Образование данной стохастической зависимости объясняется наличием (и доминированием в данном случае) постоянной части расходов по заработной плате, начисление которой не увязано с динамикой результата хозяйственной деятельности организации, т. е. выручки от продажи, а значение коэффициента детерминации, составляющее 0,64 ед. означает, что изменение расходов на оплату труда на 64 % объясняется изменением выручки от продажи, что дает основание для проведения регрессионного анализа.
Согласно виду графика, представленного на рисунке, между изучаемыми показателями существует прямолинейная корреляционная зависимость, в связи с чем уравнение регрессии будет иметь вид: Y(х) = а +b·x,
где Y – расходы на оплату труда; х – выручка от продажи товаров.
Для определения параметров а и в следует решить систему нормальных уравнений методом наименьших квадратов:
∑y = na +b∑x
∑xy = a∑x +b∑x 2 .
Отсюда значения коэффициента в определяется по формуле
Рассчитанное значение параметра в говорит о том, что при увеличении выручки от продажи товаров на 1 млн руб. расходы на оплату труда возрастут на 42,3 тыс. руб. При этом подставив значение данного параметра в первое уравнение системы, определим значение параметра а:
∑y = na +b∑x
9,639=а·28+0,0423·221,971
28а=0,0423·221,971-9,639
Значение параметра а показывает, что коэффициент регрессии может быть применим для торговых организаций с размером выручки от продажи за год свыше 9 млн. руб.
В целом уравнение регрессии имеет вид: y = 0,009+0,0423·х.
Полученное уравнение связи можно использовать для прогнозирования суммы расходов на оплату труда, если выручка от продажи возрастет и составит, например, 15 млн руб.:
y = 0,009+0,0423·х=0,009+0,0423·15=0,644 млн. руб.
7.3 Критерии оценки адекватности результатов стохастического анализа
При выполнении регрессионного анализа необходимо получить оценки, позволяющие оценить точность модели, вероятность ее существования и обоснованность применения в аналитических целях. Таким образом, качество корреляционно-регрессионного анализа обеспечивается выполнением ряда следующих условий:
1. Однородность исходной информации, которая оценивается в зависимости от относительного ее распределения около среднего значения. Критериями здесь служат (подробно см. тему 3):
– среднеквадратическое отклонение;
– коэффициент вариации;
– коэффициент равномерности;
– закон нормального распределения.
2. Значимость коэффициентов корреляции может быть оценена (наряду с уже указанным выше коэффициентом детерминации) с помощью t-критерия Стьюдента, алгоритм расчета которого при линейной однофакторной связи имеет вид:
 .
.
Если полученное эмпирическое (расчетное) значение критерия (t э) будет больше критического табличного значения (t т), то коэффициент корреляции можно признать значимым.
3. Адекватность (надежность) уравнения регрессии оценивается с помощью F-критерия Фишера, алгоритм расчета которого выглядит следующим образом:
 ,
,
где m – число параметров уравнения регрессии; σ 2 y – дисперсия по линии регрессии; σ 2 ост – остаточная дисперсия.
Если эмпирическое значение F-критерия (F э) окажется выше табличного (F т), то уравнение регрессии следует признать адекватным, т. е. правомерным для использования. При этом чем выше величина критерия Фишера, тем точнее в уравнении связи представлена зависимость, сложившаяся между факторными и результативными показателями.
4. Сравнительная сила влияния факторов, оценка которой необходима с целью определения проблемной и наиболее эффективной в перспективе зоны для направления усилий в конкретную область бизнеса. Решение этой задачи может быть осуществимо посредством использования:
а) частных коэффициентов эластичности (Э i), показывающих ожидаемый рост результативного показателя (в %) с возрастанием факторного на 1 %:

б) стандартизированных бета-коэффициентов (β i):

Чем выше бета-коэффициент, тем сильнее воздействие анализируемого фактора на результативный признак.
Тесты для самоконтроля знаний по теме 7
1. Коэффициент корреляции, равный 0, означает:
б) наличие функциональной связи прямо-пропорционального характера;
2. Коэффициент корреляции, равный (-1), означает:
а) наличие функциональной связи обратно пропорционального характера;
б) наличие функциональной связи прямо пропорционального характера;
в) отсутствие связи между фактором и изучаемым результативным показателем.
3. О наличии стохастической зависимости свидетельствует значение коэффициента корреляции, равное:
г) другие значения.
4. Аналитическая задача, которую позволяют решить методы стохастического моделирования:
а) установление факта наличия или отсутствия связи между изучаемыми признаками;
б) выявление общей тенденции изменения изучаемого показателя;
в) выбор оптимального варианта решения проблемы;
г) количественно оценка влияния факторов, находящихся с результативным показателем в функциональной зависимости.
5. Выявить тесноту связи факторных показателей и результативного позволяет:
а) корреляционный анализ;
б) регрессионный анализ;
в) детерминированный анализ.
6. Метод установления аналитического выражения (уравнения) стохастической зависимости между исследуемыми признаками – это … анализ.
7. В ходе регрессионного анализа решается следующая аналитическая задача:
а) нахождение вида зависимости между результативным показателем и независимыми факторами;
б) выявление тесноты связи факторных показателей и результативного;
в) количественная оценка влияния факторов, находящихся с результативным показателем в функциональной зависимости.
8. Для оценки достоверности полученного уравнения регрессии используют:
а) коэффициент детерминации;
б) критерий Фишера;
в) критерий Стьюдента;
г) коэффициент Кенделя;
д) коэффициент долевого участия интенсивных факторов;
е) коэффициент ритмичности;
ж) коэффициент экстенсивности.
9. При линейной однофакторной зависимости уравнение регрессии будет иметь вид:
а) y (х) = а +b·x;
б) y (х) = а +b 1 ·x 1 + b 2* x 2 +…+ b n ·x n ;
в) y (x) = a+в:х.
10. При линейной многофакторной зависимости уравнение регрессии будет иметь вид:
а) y(х) = а +b·x;
б) y (х) = а +b 1 ·x 1 + b 2 ·x 2 +…+ b n ·x n ;
в) y (x) = a+в:х.
11. В уравнении регрессии вида y(х) = а +b·x y – это:
а) результативный показатель;
б) коэффициент регрессии;
в) свободный член.
12. В уравнении регрессии вида y(х) = а +b·x а – это:
а) результативный показатель
б) коэффициент регрессии;
в) свободный член.
13. Коэффициент регрессии (b) в уравнении регрессии вида y(х) = а +b·x показывает:
а) на сколько изменится значение результативного показателя при изменении фактора на единицу;
б) величину влияния неучтенных факторов.
14. Если полученное эмпирическое (расчетное) значение критерия Стьюдента (t э) будет больше критического табличного значения (t т), то коэффициент корреляции … признать значимым.

Международной политике и законодательству. 10. Анализ должен быть эффективным, т.е. затраты на его проведение должны давать многократный эффект. 4. ЭКОНОМИЧЕСКИЙ АНАЛИЗ В ДЕЯТЕЛЬНОСТИ ОВД Содержание, цели и задачи экономико-финансового анализа, проводимого органами внутренних дел В рыночных условиях проведения социально-экономических реформ в деятельности органов внутренних дел по...
Стохастическое дифференциальное уравнение (СДУ) - дифференциальное уравнение , в котором один член или более имеют стохастическую природу, то есть представляют собой стохастический процесс (другое название - случайный процесс). Таким образом, решения уравнения также оказываются стохастическими процессами. Наиболее известный и часто используемый пример СДУ - уравнение с членом, описывающим белый шум (который можно рассматривать как пример производной винеровского процесса). Однако, существуют и другие типы случайных флуктуаций, например скачкообразный процесс .
История
В литературе традиционно первое использование СДУ связывают с работами по описанию броуновского движения , сделанными независимо Марианом Смолуховским ( г.) и Альбертом Эйнштейном ( г.). Однако, СДУ были использованы чуть ранее ( г.) французским математиком Луи Бушелье в его докторской диссертации «Теория предположений». На основе идей этой работы французский физик Поль Ланжевен начал применять СДУ в работах по физике. Позднее, он и российский физик Руслан Стратонович разработали более строгое математическое обоснование для СДУ.
Терминология
В физике СДУ традиционно записывают в форме уравнения Ланжевена. И часто, не совсем точно, называют самим уравнением Ланжевена , хотя СДУ можно записать многими другими способами. СДУ в форме уравнения Ланжевена состоит из обычного нестохастического дифференциального уравнения и дополнительной части, описывающей белый шум . Вторая распространенная форма - уравнение Фоккера-Планка , которое представляет собой уравнение в частных производных и описывает эволюцию плотности вероятности во времени. Третья форма СДУ чаще используется в математике и финансовой математике, она напоминает уравнения Ланжевена, но записано с использованием стохастических дифференциалов (см. подробности ниже).
Стохастическое исчисление
Пусть T > 0 {\displaystyle T>0} , и пусть
μ: R n × [ 0 , T ] → R n ; {\displaystyle \mu:\mathbb {R} ^{n}\times \to \mathbb {R} ^{n};} σ : R n × [ 0 , T ] → R n × m ; {\displaystyle \sigma:\mathbb {R} ^{n}\times \to \mathbb {R} ^{n\times m};} E [ | Z | 2 ] < + ∞ . {\displaystyle \mathbb {E} {\big [}|Z|^{2}{\big ]}<+\infty .}Тогда стохастическое дифференциальное уравнение при заданных начальных условиях
d X t = μ (X t , t) d t + σ (X t , t) d B t {\displaystyle \mathrm {d} X_{t}=\mu (X_{t},t)\,\mathrm {d} t+\sigma (X_{t},t)\,\mathrm {d} B_{t}} для t ∈ [ 0 , T ] ; {\displaystyle t\in ;} X t = Z ; {\displaystyle X_{t}=Z;}имеет единственное (в смысле «почти наверное») и t {\displaystyle t} -непрерывное решение (t , ω) ∣ → X t (ω) {\displaystyle (t,\omega)\shortmid \!\to X_{t}(\omega)} , такое что X {\displaystyle X} - адаптированный процесс к фильтрации F t Z {\displaystyle F_{t}^{Z}} , генерируемое Z {\displaystyle Z} и B s {\displaystyle B_{s}} , s ≤ t {\displaystyle s\leq t} , и
E [ ∫ 0 T | X t | 2 d t ] < + ∞ . {\displaystyle \mathbb {E} \left[\int \limits _{0}^{T}|X_{t}|^{2}\,\mathrm {d} t\right]<+\infty .}Применение стохастических уравнений
Физика
В физике СДУ часто записывают в форме уравнения Ланжевена. Например, систему СДУ первого порядка можно записать в виде:
x ˙ i = d x i d t = f i (x) + ∑ m = 1 n g i m (x) η m (t) , {\displaystyle {\dot {x}}_{i}={\frac {dx_{i}}{dt}}=f_{i}(\mathbf {x})+\sum _{m=1}^{n}g_{i}^{m}(\mathbf {x})\eta _{m}(t),}где x = { x i | 1 ≤ i ≤ k } {\displaystyle \mathbf {x} =\{x_{i}|1\leq i\leq k\}} - набор неизвестных, f i {\displaystyle f_{i}} и - произвольные функции, а η m {\displaystyle \eta _{m}} - случайные функции от времени, которые часто называют шумовыми членами. Такая форма записи используется, так как существует стандартная техника преобразования уравнения со старшими производными в систему уравнений первого порядка с помощью введения новых неизвестных. Если g i {\displaystyle g_{i}} - константы, то говорят, что система подвержена аддитивному шуму. Также рассматривают системы с мультипликативным шумом, когда g (x) ∝ x {\displaystyle g(x)\propto x} . Из этих двух рассмотренных случаев аддитивный шум - проще. Решение системы с аддитивным шумом часто можно найти используя только методы стандартого математического анализа . В частности, можно использовать обычный метод композиции неизвестных функций. Однако, в случае мультипликативного шума уравнение Ланжевена плохо определено в смысле обычного математического анализа и его необходимо интерпретировать в терминах исчисления Ито или исчисления Стратоновича.
В физике основным методом решения СДУ является поиск решения в виде плотности вероятности и преобразованием первоначального уравнения в уравнение Фоккера-Планка . Уравнение Фоккера-Планка - дифференциальное уравнение в частных производных без стохастических членов. Оно определяет временную эволюцию плотности вероятности, также как уравнение Шрёдингера определяет зависимость волновой функции системы от времени в квантовой механике или уравнение диффузии задает временную эволюцию химической концентрации. Также решения можно искать численно, например с помощью метода Монте-Карло . Другие техники нахождения решений используют интеграл по путям , эта техника базируется на аналогии между статистической физикой и квантовой механикой (например, уравнение Фоккера-Планка можно преобразовать в уравнение Шрёдингера с помощью некоторого преобразования переменных), или решением обыкновенных дифференциальных уравнений для моментов плотности вероятности.
Ссылки
- Стохастический мир - простое введение в стохастические дифференциальные уравнения
Литература
- Adomian, George. Stochastic systems (неопр.) . - Orlando, FL: Academic Press Inc., 1983. - (Mathematics in Science and Engineering (169)).
- Adomian, George. Nonlinear stochastic operator equations (неопр.) . - Orlando, FL: Academic Press Inc., 1986.
- Adomian, George. Nonlinear stochastic systems theory and applications to physics (англ.) . - Dordrecht: Kluwer Academic Publishers Group , 1989. - (Mathematics and its Applications (46)). (англ.)
Существенной особенностью социально-экономических процессов является невозможность однозначно предсказать их ход на основе имеющейся априори информации. Несмотря на то, что социально-экономические процессы подчиняются определенным объективным законам, в каждом конкретном процессе эти законы проявляются через множество неопределенностей .
Математическая же модель процесса может содержать либо детерминированные параметры и связи, либо стохастические, но не может (по крайней мере, при нынешнем состоянии науки) содержать неопределенности.
Выбор детерминированного либо стохастического подхода к моделированию того или иного социально-экономического процесса зависит от целей моделирования, возможной точности определения исходных данных, требуемой точности результатов и отражает информацию исследователя о природе причинно-следственных связей реального процесса. При этом неопределенные факторы, которые могут иметь место в реальных процессах, должны быть приближенно представлены как детерминированные или стохастические. Характер параметров, входящих в модель, относится к тем исходным допущениям, которые могут быть обоснованы только эмпирическим путем. Соответствующая гипотеза о детерминированном или стохастическом характере параметров и связей модели принимается в том случае, если она в пределах требуемой или возможной точности определения этих параметров не противоречит опытным данным.
Большинство современных моделей социально-экономических процессов основано на теоретико-вероятностных конструкциях . В связи с этим целесообразно рассмотреть вопрос об исходных посылках применимости таких конструкций к моделированию.
Теория вероятностей изучает математические модели экспериментов (реальных явлений), исход которых не вполне однозначно определяется условиями опыта. Поэтому неоднозначность социально-экономических процессов часто является решающей в выборе стохастического (вероятностного) подхода к их моделированию. Вместе с тем не всегда учитывается, что аппарат теории вероятностей применим для описания и изучения не любых экспериментов с неопределенными исходами, а лишь экспериментов, исходы которых обладают статистической устойчивостью . Тем самым важнейший вопрос об эмпирическом обосновании применимости теоретико-вероятностных методов к рассматриваемым конкретным характеристикам социально-экономических процессов иногда полностью выпадает из поля зрения.
Применимость методов теории вероятностей для исследования тех или иных процессов может быть обоснована только эмпирически на основе анализа статистической устойчивости характеристик этих процессов.
Статистическая устойчивость представляет собой устойчивость эмпирического среднего, частоты события или каких-либо других характеристик протокола измерений исследуемого параметра того или иного процесса.
Следует, однако, отметить, что вопрос о статистической устойчивости реального социально-экономического процесса в целом, а, следовательно, и о применимости теоретико-вероятностных понятий к его моделированию, в настоящее время может быть решен только на интуитивном уровне. Это объективно обусловлено отсутствием достаточного числа опытов, касающихся процесса в целом. Вместе с тем большинство «элементарных» процессов, составляющих тот или иной социально-экономический процесс, носят случайный характер (т.е. гипотеза об их статистической устойчивости не противоречит имеющемуся опыту). Так, например, факт покупки того или иного количества конкретного товара за установленный период времени достаточно часто является случайным событием. Случайным является количество родившихся детей. Случайный характер носят процессы потребления. Случайными являются отказы техники, моральное состояние людей, участвующих в производстве товаров и услуг и т.д. Случайность этих явлений эмпирически подтверждена достаточно большим числом экспериментов.
Все указанные «элементарные» случайные процессы взаимодействуют между собой, объединяясь в едином социально-экономическом процессе. Несмотря на то, что управление в социально-экономической сфере направлено на снижение элемента случайности и придание этому процессу детерминированного целенаправленного характера, реальные процессы столь сложны, что как бы ни была высока степень централизации управления, случайные факторы в них всегда присутствуют. Поэтому природа социально-экономических процессов остается случайной в широком смысле. Это служит основанием для применения стохастических моделей при их исследовании, хотя полную стохастическую устойчивость того или иного процесса в целом вряд ли можно вполне гарантировать.
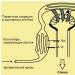
В настоящее время сложились два основных подхода к стохастическому моделированию социально-экономических процессов (рис. 4.8). Первое направление связано с построением стохастических моделей на основе метода статистических испытаний (Монте-Карло). Второе направление заключается в построении аналитических моделей. Оба эти направления развиваются параллельно и взаимно дополняют друг друга.
Главной особенностью моделей, основанных на методе статистических испытаний, является то, что они приближенно воспроизводят социально-экономический процесс на основе имитации его элементарных составляющих и их взаимосвязей. Это позволяет моделировать процессы очень сложной структуры, зависящие от большого числа разнообразных факторов. Вместе с тем модели статистических испытаний, как правило, громоздки. Их применение требует большого объема памяти ЭВМ и связано с большими затратами машинного времени. Существенным недостатком этих моделей также является отсутствие конструктивных способов оптимизации.
Некоторые из недостатков имитационных статистических моделей социально-экономических процессов преодолеваются применением аналитических моделей.
Рис. 4.8. Стохастическое моделирование социально-экономических процессов
В настоящее время для построения аналитических моделей стохастических процессов применяются два основных подхода – микроскопический и макроскопический.
Микроскопический подход состоит в детальном изучении поведения каждого элемента социально-экономической системы.
Макроскопические модели изучают только макросвойства системы и учитывают только средние характеристики состояния системы, например, среднее количество элементов системы, находящихся в некотором определенном состоянии. Это приводит к потере информации о состоянии каждого элемента социально-экономической системы, так как одни и те же макросостояния могут быть результатом различных сочетаний микросостояний. В то же время макроскопический подход позволяет сократить размерность математической модели, сделать ее более обозримой, сократить затраты ресурсов ЭВМ при производстве расчетов. Микроскопический подход предпочтителен в случае, когда требуется более детальная информация о поведении системы. Макроскопический подход применяется для достаточно быстрых оценочных расчетов.
Отличительная черта детерминированной модели состоит в том, что при заданных параметрах и начальных условиях процесс полностью определен для любого момента времени t > 0.
При стохастической трактовке модель описывает динамику вероятностных характеристик (например, математических ожиданий) процесса и, следовательно, характеризует процесс в среднем, представляя лишь оценки для каждой конкретной реализации. Стохастические модели социально-экономических процессов позволяют предсказать только средние результаты (моменты распределения результатов процесса) или вероятности наступления тех или иных результатов.
Стохастическая модель описывает ситуацию, когда присутствует неопределенность. Другими словами, процесс характеризуется некоторой степенью случайности. Само прилагательное «стохастический» происходит от греческого слова «угадывать». Поскольку неопределенность является ключевой характеристикой повседневной жизни, то такая модель может описывать все что угодно.
Однако каждый раз, когда мы ее применяем, будет получаться разный результат. Поэтому чаще используются детерминированные модели. Хотя они и не являются максимально приближенными к реальному положению вещей, однако всегда дают одинаковый результат и позволяют облегчить понимание ситуации, упрощают ее, вводя комплекс математических уравнений.
Основные признаки
Стохастическая модель всегда включает одну или несколько случайных величин. Она стремится отразить реальную жизнь во всех ее проявлениях. В отличие от стохастическая не имеет цели все упростить и свести к известным величинам. Поэтому неопределенность является ее ключевой характеристикой. Стохастические модели подходят для описания чего угодно, но все они имеют следующие общие признаки:
- Любая стохастическая модель отражает все аспекты проблемы, для изучения которой создана.
- Исход каждого из явлений является неопределенным. Поэтому модель включает вероятности. От точности их расчета зависит правильность общих результатов.
- Эти вероятности можно использовать для прогнозирования или описания самих процессов.
Детерминированные и стохастические модели
Для некоторых жизнь представляется чередой для других - процессов, в которых причина обуславливает следствие. На самом же деле для нее характерна неопределенность, но не всегда и не во всем. Поэтому иногда трудно найти четкие различия между стохастическими и детерминированными моделями. Вероятности являются достаточно субъективным показателем.

Например, рассмотрим ситуацию с подбрасыванием монетки. На первый взгляд кажется, что вероятность того, что выпадет «решка», составляет 50%. Поэтому нужно использовать детерминированную модель. Однако на деле оказывается, что многое зависит от ловкости рук игроков и совершенства балансировки монетки. Это означает, что нужно использовать стохастическую модель. Всегда есть параметры, которые мы не знаем. В реальной жизни причина всегда обуславливает следствие, но существует и некоторая степень неопределенности. Выбор между использованием детерминированной и стохастической моделей зависит от того, чем мы готовы поступиться - простотой анализа или реалистичностью.
В теории хаоса
В последнее время понятие о том, какая модель называется стохастической, стало еще более размытым. Это связано с развитием так называемой теории хаоса. Она описывает детерминированные модели, которые могут давать разные результаты при незначительном изменении исходных параметров. Это похоже на введение в расчет неопределенности. Многие ученые даже допустили, что это уже и есть стохастическая модель.

Лотар Брейер изящно объяснил все с помощью поэтических образов. Он писал: «Горный ручеек, бьющееся сердце, эпидемия оспы, столб восходящего дыма - все это является примером динамического феномена, который, как кажется, иногда характеризуется случайностью. В реальности же такие процессы всегда подчинены определенному порядку, который ученые и инженеры еще только начинают понимать. Это так называемый детерминированный хаос». Новая теория звучит очень правдоподобно, поэтому многие современные ученые являются ее сторонниками. Однако она все еще остается мало разработанной, и ее достаточно сложно применить в статистических расчетах. Поэтому зачастую используются стохастические или детерминированные модели.
Построение
Стохастическая начинается с выбора пространства элементарных исходов. Так в статистике называют перечень возможных результатов изучаемого процесса или события. Затем исследователь определяет вероятность каждого из элементарных исходов. Обычно это делается на основе определенной методики.

Однако вероятности все равно являются достаточно субъективным параметром. Затем исследователь определяет, какие события представляются наиболее интересными для решения проблемы. После этого он просто определяет их вероятность.
Пример
Рассмотрим процесс построения самой простой стохастической модели. Предположим, мы кидаем кубик. Если выпадет «шесть» или «один», то наш выигрыш составит десять долларов. Процесс построения стохастической модели в этом случае будет выглядеть следующим образом:
- Определим пространство элементарных исходов. У кубика шесть граней, поэтому могут выпасть «один», «два», «три», «четыре», «пять» и «шесть».
- Вероятность каждого из исходов будет равна 1/6, сколько бы мы ни подбрасывали кубик.
- Теперь нужно определить интересующие нас исходы. Это выпадение грани с цифрой «шесть» или «один».
- Наконец, мы может определить вероятность интересующего нас события. Она составляет 1/3. Мы суммируем вероятности обоих интересующих нас элементарных событий: 1/6 + 1/6 = 2/6 = 1/3.
Концепция и результат
Стохастическое моделирование часто используется в азартных играх. Но незаменимо оно и в экономическом прогнозировании, так как позволяют глубже, чем детерминированные, понять ситуацию. Стохастические модели в экономике часто используются при принятии инвестиционных решений. Они позволяют сделать предположения о рентабельности вложений в определенные активы или их группы.

Моделирование делает финансовое планирование более эффективным. С его помощью инвесторы и трейдеры оптимизируют распределение своих активов. Использование стохастического моделирования всегда имеет преимущества в долгосрочной перспективе. В некоторых отраслях отказ или неумение его применять может даже привести к банкротству предприятия. Это связано с тем, что в реальной жизни новые важные параметры появляются ежедневно, и если их не может иметь катастрофические последствия.
Стохастические модели описывают случайные процессы или ситуации, при этом подразумевается, что случайность тех или иных явлений выражается в терминах вероятности. Так же, как и детерминированные, стохастические модели бывают дискретные и непрерывные.
Непрерывно-стохастические модели
Основной схемой формализованного описания систем, для которых характерны
1) непрерывный характер изменения времени и
2) наличие случайностей в поведении,
служит аппарат систем массового обслуживания. То есть это план математических схем, разработанных для формализации процессов функционирования систем, которые являются процессами обслуживания. Именно для таких систем характерны стохастический характер функционирования (случайное появление заявок на обслуживание), завершение обслуживания в случайные моменты времени, наличие входного и выходного потока заявок, наличие приборов обслуживания, поток событий, существование очереди на обслуживание, определение некоторого порядка обслуживания и т.п.
Как видно из описания моделей такого рода, непрерывно-стахостические модели нам не подходят.
Дискретно-стохастические модели
Данный тип моделей подходит для тех объектов, которые обладают следующими характеристиками:
время в них дискретно
они проявляют статически закономерное случайное поведение.
По данному определению наша модель полностью подходит под описание дискретно-стохастических моделей: по условию время у нас дискретно и мы сделали вывод, что в модели присутствуют случайности. Модели систем такого рода могут быть построены на основе двух схем формализованного описания:
Конечно-разностные уравнения, среди переменных которых используют функции, задающие случайные процессы
Вероятностные автоматы
“Вероятностным автоматом называется дискретный прелбразователь информации, имеющий более одного состояния, функционирование которого в каждом такте зависит только от состояния памяти в нем и может быть описано статически” 3
Задание вероятностных автоматов осуществляется таблично или с помощью графов, но их использование на практике возможно лишь путем реализации имитационной модели на ЭВМ (за исключением небольших и несложных моделях, при которых возможны и аналитические расчеты).
Проверим возможность применения вероятностных автоматов к нашей модели:
Случайности в нашей модели есть, но представляется ли возможным вычислить закон распределения?
1.В случае случайной цены?
Да, это равномерное распределение и вероятности всех состояний при определении цены равны.
В случае случайного распределения непроданной продукции?
Это опять равномерное распределение и вероятности найти можно.
Посмотрим, какие входные состояния может принимать система...Оказывается таких состояний бесконечно много, следовательно, вероятностный автомат построить нельзя. А если сделать ограничения на объем выпуска? Это множество будет конечным и вероятностный автомат можно будет построить, но полученная модель, как и в случае предположения о детерминированности системы, будет плохо отражать реальность. Поэтому откажемся от построения вероятностного автомата.
Наиболее удобным в случае дискретно-стохастической схемы формализованного описания представляется решение задачи с помощью конечно-разностных уравнений.