Основные типовые динамические звенья систем автоматического управления. Типовые элементарные звенья систем автоматического управления

Передаточная функция звена в общем случае представляет собой отношение двух полиномов:

Полином произвольного порядка можно разложить на простые множители k 1 p ; (d 1 p + d 2 ); (d 1 p 2 + d 2 p + d 3 ), поэтому передаточную функцию можно представить как произведение простых множителей или простых дробей вида:

;
;
.

Звенья, передаточные функции которых имеют вид простых множителей или простых дробей, называют типовыми или элементарными звеньями. Элементарные множители, представляющие собой полиномы первого и второго порядка, преобразовываются к стандартному виду, принятому в теории автоматического управления:

;
,

k (k  0) - коэффициент передачи ,

T (T  0) - постоянная времени (имеет размерность единицы времени),

 - коэффициент демпфирования (затухания) .

Основные типы звеньев делятся на: позиционные, дифференцирующие и интегрирующие.

Позиционными з веньями называются такие звенья, в передаточной функции которых многочлены M (p ) и N (р ) имеют свободные члены.

У дифференцирующих звеньев в передаточной функции отсутствует свободный член числителя, т.е. для однократно дифференцирующих звеньев передаточная функция имеет вид:

, где M 1 (p ) - свободный член.

У интегрирующих звеньев в передаточной функции отсутствует свободный член знаменателя, т.е.:

.

1. Апериодическое звено . Стандартная форма записи уравнения звена:

А

а ) б )

Рисунок 13. Схемы реализации

апериодического звена

периодическими звеньями являютсяRC и RL цепи, входные и выходные величины которых показаны соответственно на рисунке 13, а и 13, б .

В операторной форме напряжение и ток на выходе для схемы (рис. 13, а ) соответственно равны:

и

.

Рисунок 14. Характеристики

апериодического звена первого порядка

Передаточная функция апериодического звена:

В общем случае передаточная функция апериодического звена имеет вид:

где: k = 1, T = RC .

Переходная функция апериодического звена (рис. 14,а ):

.

Весовая функция апериодического звена (рис. 14,б ):

Если характеристики этих функций получены экспериментально, по ним можно определить значения T и k и получить уравнение звена. За длительность переходного процесса принимают время, в течение которого выходная величина достигает 95% ее конечного значения.

Амплитудно-фазовая частотная характеристика (АФЧХ) апериодического звена (рис. 14,в ):

где:
,
.

Эта характеристика представляет собой полуокружность с радиусом k /2 и центром с координатами (k /2; j = 0) на действительной оси.

Амплитудно-частотная (АЧХ) апериодического звена:

Фазовая частотная характеристики (ФЧХ) апериодического звена:

Логарифмическая амплитудная частотная характеристика (ЛАЧХ) апериодического звена (рис. 14,г ):

Приближенно ЛАЧХ можно заменить двумя асимптотами, к которым она стремится при  → 0 и  → . Приближенная ЛАЧХ называется асимптотической .

Обе асимптоты пересекаются в точке, соответствующей  = 1/T . Эта частота называется сопрягающей .

На фазовой частотной характеристике (ФЧХ) при  →  значение φ изменяется от 0 до минус π/2.

2. Колебательное звено . Уравнение колебательного звена имеет вид:
.

Рисунок 15. Схема реализации

колебательного звена

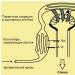
Оно представляет собой последовательное соединение RLC элементов (рис. 15 ).

В операторной форме напряжение на выходе колебательного звена:

, где:
,
.

Принято обозначать Т 0 = Т , Т 1 = 2ξТ , тогда передаточная функция колебательного звена имеет вид:

Коэффициент ξ (дзета) называется коэффициентом демпфирования (затухания). Если 0 < ξ < 1, звено называется колебательным; если ξ = 0 (Т 1 = 0), звено называется консервативным , если ξ ≥ 1 - апериодическим звеном второго порядка.

А

Рисунок 16. Характеристики

колебательного звена

периодическое звено второго порядка можно представить как последовательное соединение двух апериодических звеньев первого порядка. Оно не относится к числу элементарных звеньев.

В общем случае амплитудно-фазовая частотная характеристика звена (рис. 16,а ):

где k = 1.

Умножив числитель и знаменатель на комплексно сопряженное знаменателю выражение, получим:

Отсюда вещественная и мнимая частотные характеристики колебательного звена:

и

Амплитудно-частотная характеристика колебательного звена (АЧХ):

Логарифмическая амплитудно-частотная характеристика (ЛАЧХ) колебательного звена:

При малых значениях частоты ω<1/Т = ω с в выражении
можно пренебречь величинойТ 2 ω 2 , а при значениях частоты ω>1/Т в выражении
можно пренебречь единицей и слагаемым (2ξТω ) 2 . Тогда уравнение асимптотической ЛАЧХ колебательного звена можно записать:

Асимптотическая ЛАЧХ (рис. 16,б ) при ω<1/Т = ω с (ω с - сопрягаемая частота) параллельна оси частот, а при ω ≥ 1/Т имеет наклон минус 40 дБ/декаду. При значениях 0,5<ξ<1 характеристика близка к ломанной линии, если ξ<0,5, то получается заметный «горб», который уходит в бесконечность при ξ → 0. Роль постоянных времени Т 0 и Т 1 в уравнении колебательного звена следующая: постоянная Т 0 - «раскачивает» колебания, а Т 1 - демпфирует их.

Фазовая частотная характеристика (ФЧХ) (рис. 16,б ) изменяется монотонно в интервале от 0 до -  :

Переходная функция колебательного звена (рис. 16,в ) при нулевых начальных условиях:

,

где:
;
;
.

При
переходная характеристика представляет собой график гармонических колебаний.

Весовая функция колебательного звена :

Все элементы системы независимо от их конструктивного исполнения и назначения по своим динамическим свойствам можно подразделить на ограниченное число типовых динамических. Под типовым динамическим звеном понимают элемент системы направленного действия, описываемый в динамике дифференциальным уравнением не выше второго порядка или алгебраическим уравнением. Классифицируют звенья именно по виду уравнения динамики.

Все звенья можно разделить на два типа: минимально-фазовые и неминимально-фазовые.

Звено является неминимально-фазовым, если его передаточная функция имеет положительные нули или полюса, у таких звеньев фазовая характеристика не соответствует дифференциальному уравнению. Для минимально-фазовых звеньев фазочастотная характеристика однозначно определяется амплитудно-частотной характеристикой.

Динамические звенья могут быть устойчивыми, если после приложения и снятия воздействия его выходная переменная стремится к значению до момента приложения воздействия (т.е. возвращается в исходное состояние); нейтральными (астатическими), если при ступенчатом воздействии выходная переменная изменяется с постоянной скоростью (астатизм первого порядка) или постоянным ускорением (астатизм второго порядка); а после приложения и снятия воздействия приходит в новое устойчивое состояние; неустойчивые, если выходная переменная после приложения и снятия возмущения изменяется, не приходя к некоторому устойчивому состоянию.

Рассмотрим минимально-фазовые звенья. По типу уравнений динамики их можно классифицировать следующим образом.

Простейшие звенья: а) безынерционное (усилительное, пропорциональное); б) идеально-интегрирующее, идеально-дифференцирующее;

Звенья первого порядка: а) инерционное звено первого порядка (апериодическое); б) форсирующее звено; в) реально-дифференцирующее звено первого порядка; г) интегро-дифференцирующее (инерционно-форсирующее) первого порядка.

Звенья второго порядка: а) апериодическое (инерционное) звено второго порядка; б) колебательное; в) консервативное.

Особые звенья: звено запаздывания и иррациональные звенья.

Рассмотрим типовые звенья, их уравнения динамики, передаточные функции и характеристики.

§1. Простейшие звенья.

1) Безынерционное звено.

Выходной сигнал этого звена по форме повторяет входной сигнал. Уравнение динамики

K - коэффициент пропорциональности, который может быть определен по статической характеристике

Уравнение звена в изображениях

и передаточная функция

Получим, заменив в выражении передаточной функции оператор Лапласа p на оператор Фурье jщ.

(реакция на ступенчатый сигнал)

Рисунок 3.1

Реакция на импульс

Звено устойчивое.

АФЧХ получим изменяя частоту от нуля до бесконечности. Из выражения W(jщ) видно, что комплексный коэффициент усиления не зависит от частоты и не будет смещения вектора W(jщ). Таким образом АФЧХ этого звена представляет собой точку на вещественной оси, отстоящую на расстояние K от начала координат.

Рисунок 3.2

Логарифмические амплитудно и фазочастотные характеристики:

Таким образом ЛАЧХ пройдет параллельно оси частот на расстоянии от нее (20 Lg K) определяемым коэффициентом передачи, фазовый сдвиг во всем диапазоне частот равен нулю.

Рисунок 3.3

Примеры безынерционных звеньев: зубчатая передача, рычажная передача, делитель напряжения, усилитель.

2) Идеально-интегрирующее звено.

Выходной сигнал этого звена равен интегралу от входного, уравнение динамики имеет следующий вид:

Где - время интегрирования.

Передаточная функция звена

Перейдем к выражению комплексного коэффициента передачи:

Временные характеристики:

а) переходная функция и характеристика

Рисунок 3.4

б) функция веса и импульсная переходная характеристика

Рисунок 3.5

По импульсной переходной характеристике видно, что звено астатическое (астатизм первого порядка), после снятия возмущения выходная переменная приходит к новому установившемуся значению.

Частотные характеристики.

Амплитудно-фазовая частотная характеристика

представляет собой отрицательный отрезок мнимой полуоси.

Рисунок 3.6

Логарифмические частотные характеристики.

ЛАЧХ определяется выражением

и представляет собой прямую с отрицательным угловым коэффициентом. При щ=1 , точка пересечения с осью lg соответствует уравнению

20lgK - 20lg = 0, lg = lg K, т.е. = K.

Поэтому ее можно построить рассчитав значение L(= 1) = 20lgK и через эту точку провести прямую с наклоном -20Дб/дек, или через точку lg=lgK.

Рисунок 3.7

Уравнение фазовой характеристики, т.е. фазовый сдвиг, постоянен и не зависит от частоты, а характеристика ФЧХ параллельна оси частот.

Наклон ЛАЧХ -20Дб/дек означает, что с увеличением частоты в 10 раз (1 декада) модуль амплитудной характеристики уменьшается на 20 Дб (в 10 раз).

Примеры звена:

3) Идеально-дифференцирующее звено.

Выходной сигнал этого звена пропорционален скорости изменения входного сигнала и уравнение звена

Уравнение в изображениях

Передаточная функция звена

Комплексный коэффициент передачи

Временные характеристики

а) переходная функция и характеристика

Рисунок 3.9

б) функция вес и импульсная переходная характеристика

Два импульса противоположной полярности.

Частотные характеристики.

АФЧХ строится по выражению и представляет собой положительный отрезок мнимой оси. .

Рисунок 3.10

Логарифмические характеристики

ЛАЧХ строится по выражению и представляет собой прямую с положительным угловым коэффициентом, она пересекает ось lgщ в точке

На частоте щ=1 L(щ) = 20lgK.

Таким образом, ЛАЧX можно построить рассчитав точку и отложив ее на оси lgщ провести прямую с наклоном +20Дб/дек или через точку (при щ=1) 20lgK с тем же наклоном.

Рисунок 3.11

наклон +20Дб/дек, означает, что с увеличением частоты в 10 раз модуль амплитудной характеристики увеличивается на 20Дб (в 10 раз).

Уравнение фазовой характеристики - т.е. фазовый сдвиг не зависит от частоты и ФЧХ проходит параллельно оси lgщ через отметку +90є.

§2. Звенья первого порядка.

Апериодическое (инерционное) звено первого порядка.

Это звено в динамике описывается дифференциальным уравнением первого порядка.

где T - постоянная времени, характеризующая инерционные свойства звена;

K - коэффициент пропорциональности, характеризует статизм звена (коэффициент статизма).

Запишем уравнение в изображениях

передаточная функция;

Заменой p на jщ перейдем к комплексному коэффициенту передачи

Временные характеристики звена

а) Переходная функция и характеристика

Уравнение экспоненты;

Корень характеристического уравнения > Tp +1 = 0

Рисунок 3.13

Согласно уравнению переходной характеристики h(t=T)=0,63K, т.е. за время равное одной постоянной времени выходная переменная достигает 0,63 от установившегося значения h(?).

h(t=3T) = 0,95 h(?); h(t=4T) = 0,98 h(?), т.е. переходный процесс за время равное 4T можно считать завершившимся (tпер=(3ч4)T).

Постоянную времени можно определить по графику h(t) (как показано на рисунке) используя свойство экспоненты - проекция под касательной на линию установившегося значения равна постоянной времени или определяя время за которое h(t) достигает значение 0,63 h(?).

Рисунок 3.14

В соответствии с видом временных характеристик звено является устойчивым.

Частотные характеристики.

Амплитудно-фазовая частотная характеристика строится по выражению при изменении частоты 0 < щ < ?. АФЧХ этого звена согласно уравнению, представляет собой полуокружность диаметром K, расположенную в четвертом квадранте.

Рисунок 3.15

При увеличении частоты вектор W(jщ) смещается по часовой стрелке и фазовый сдвиг меняется нуля до -90є.

Логарифмические характеристики.

Обычно строят асимптотические ЛАЧХ, которые представляют собой ломаные линии и очень легко рассчитываются. На низких частотах, второе слагаемое в выражении (*) очень мало и его можно не учитывать, при второе слагаемое дает значение 10lg2 = 3,01, а при увеличении частоты его вклад возрастает.

Поэтому асимптотическую ЛАЧХ строят следующим образом:

для частоты по уравнению - прямая параллельна оси частот;

для наклонную линию с наклоном -20 Дб/дек. Ошибка на частоте равна 3Дб, т.е. точная L(щ) на этой частоте проходит ниже на 3Дб (показана пунктиром).

Рисунок 3.16

Фазовая характеристика

Примеры звена:

Дифференциальным уравнением первого порядка описываются переходные процессы в магнитном усилителе (инерционный усилитель), тепловые процессы, процессы растворения и осаждения и другие технологические процессы.

Остальные звенья первого порядка можно рассматривать как соединения простейших звеньев и звена апериодического или как соединение простейших звеньев.

Форсирующее звено.

Рисунок 3.19

K1 - размерный коэффициент (сек.), K2 - безразмерный.

т.е. выходной сигнал пропорционален входному и скорости его изменения.

Комплексный коэффициент передачи

Временные характеристики звена

а)переходная функция и характеристика

Рисунок 3.20

б) функция веса и импульсная переходная характеристика

Рисунок 3.21

Звено устойчивое

Частотные характеристики

Амплитудно-фазовая частотная характеристика строится по выражению

при изменении частоты 0 < щ < ? и представляет собой вертикальную прямую отстоящую от начала коорлинат на величину K.

Рисунок 3.22

Логарифмическая амплитудно-частотная характеристика >

Асимптотическая ЛАЧХ - ломаная линия, на первом участке до - прямая параллельная оси частот и отстоящая от нее на расстояние 20lgK, на частоте происходит излом и дальше характеристика проходит с наклоном +20 Дб/дек.

Рисунок 3.23

Реально-дифференцирующее звено

Это звено можно рассматривать как последовательное соединение идеально-дифференцирующего звена и апериодического первого порядка или как встречно-параллельное соединение безынерционного и идеально-интегрирующего звеньев.

Дифференциальное уравнение звена

Уравнение в изображениях и передаточная функция

Комплексный коэффициент передачи

Временная характеристика звена

а) переходная функция и характеристика

т.е. аналогична функции веса апериодического звена первого порядка.

Рисунок 3.26

б) функция веса и импульсная переходная характеристика.

Рисунок 3.27

Частотные характеристики.

Амплитудно-фазовая частотная характеристика при 0 < щ < ?, представляет собой полуокружность диаметром в первом квадранте.

Рисунок 3.28

Логарифмическая асимптотическая амплитудно-частотная характеристика представляет собой ломаную линию, до - наклон +20 Дб/дек далее прямая параллельна оси частот.

и может быть получена как сумма ЛАЧХ двух последовательно соединенных апериодического и идеально-дифференцирующего звена.

Рисунок 3.29

Инерционно-форсирующее (интегро-дифференцирующее) звено.

Может быть получено как последовательное соединение апериодического первого порядка и форсирующего звена или встречно-параллельного соединения усилителя и апериодического звена первого порядка.

Дифференциальное уравнение звена:

Уравнение в изображениях и передаточная функция

Комплексный коэффициент передачи

Свойства этого звена зависят от соотношения постоянных времени, если < 1 то звено по своим свойствам приближается к инерционному звену, а если > 1 - к дифференцирующему.

Временные характеристики звена.

а) переходная функция и характеристики.

Рисунок 3.34

б) функция веса и импульсная переходная характеристика.

Рисунок 3.35

Частотные характеристики звена.

Амплитудно-фазовая частотная характеристика строится по выражению при изменении частоты от нуля до бесконечности и вид ее также зависит от соотношения.

Рисунок 3.36

Логарифмические характеристики асимптотическая амплитудная также представляет собой ломаные линии и зависят от коэффициента в.

Рисунок 3.37

Неминимально-фазовые звенья

Звено является неминимально-фазовым звеном, если сдвиг по фазе при 0 < щ < ? превышает максимально возможное значение для данного типа уравнения динамики.

Звено является неминимально-фазовым, если его W(p) имеет положительный нуль или полюс (корень полинома числителя или знаменателя). Одной и той же АЧХ звена может соответствовать разные ФЧХ.

Устойчивое неминимально-фазовое инерционное звено первого порядка

Уравнение:

имеем положительный нуль

Корень положительное число.

при 0 < щ < ?, ц(щ) меняется от 0 до -180є.

Временные характеристики.

при T2 > T1

Рисунок 3.38

Частотные характеристики: АФЧХ T2 > T1

Рисунок 3.39

ЛАЧХ - - уравнение такое же как у инерционно-форсирующего звена.

Рисунок 3.40

Апериодическое неустойчивое неминимально-фазовое звено.

Уравнение:

Начало в третьем квадранте.

Рисунок 3.41

ЛАЧХ - - как у апериодического устойчивого.

Рисунок 3.42

Неустойчивое неминимально-фазовое звено второго порядка.

Уравнение:

Частотные характеристики - расходящиеся колебания.

Рисунок 3.43

ЛАЧХ - уравнение как у колебательного звена.

Рисунок 3.44

о < 0,3 - использовать номограммы поправок.

К неминимально-фазовым относятся звенья:

Неустойчивое

Неустойчивое

Устойчивое

и другие.

Особое звено (также неминимально-фазовое)

Звено запаздывания (чистого запаздывания)

Уравнение:

Не зависит от щ.

ц(щ) при изменении частоты меняется от 0 до -?.

Временные характеристики. Звено повторяет входной сигнал без искажения, но со сдвигом во времени:

Рисунок 3.45

Частотные характеристики:

АФЧХ - окружность первого радиуса.

Рисунок 3.46

ЛАЧХ - - совпадает с осью частот, а ц(щ) - от 0 до -?.

Рисунок 3.47

Примеры звеньев: устройства считывания и записи информации, длинные линии электропередачи, гидротрубопроводы, транспортные линии.

В следящих системах (рис. 1.14, а) при повороте ведущего вала на некоторый угол приемный вал также поворачивается на этот же угол. Однако приемный вал занимает новое положение не мгновенно, а с некоторым запозданием после окончания переходного процесса. Переходный процесс может быть апериодическим (рис. 2.1, а) и колебательным с затухающими колебаниями (рис. 2.1, б). Возможно, что колебания приемного вала будут незатухающими (рис. 2.1, в) или возрастающими по амплитуде (рис. 2.1, г). Последние два режима являются неустойчивыми.

Каким образом данная система будет отрабатывать то или иное изменение задающего или возмущающего воздействия, т. е. каков характер переходного процесса системы, будет ли система устойчивой или неустойчивой - эти и подобные вопросы рассматриваются в динамике систем, автоматического управления.

2.1. Динамические звенья автоматических систем

Необходимость представления элементов автоматических систем динамическими звеньями. Определение динамического звена

Для определения динамических свойств автоматической системы необходимо иметь ее математическое описание, т. е. математическую модель системы. Для этого следует составить дифференциальные уравнения элементов системы, с помощью которых описываются происходящие в них динамические процессы.

При анализе элементов автоматических систем выясняется, что разнообразные элементы, отличающиеся назначением, конструкцией, принципом действия и физическими процессами, описываются одинаковыми дифференциальными уравнениями, т. е. являются сходными по динамическим свойствам. Например, в электрической цепи и механической системе, несмотря на различную их физическую природу, динамические процессы могут описываться аналогичными дифференциальными уравнениями.

Рис. 2.1. Возможные реакции следящей системы на ступенчатое задающее воздействие.

В теории автоматического управления элементы автоматических систем с точки зрения их динамических свойств представляют с, помощью небольшого числа элементарных динамических звеньев. Под элементарным динамическим звеном понимается математическая модель искусственно выделяемой части системы, характеризуемая нексь торым простейшим алгоритмом (математическим или графическим описанием процесса).

Одним элементарным звеном иногда могут быть представлены несколько элементов системы или наоборот - один элемент может быть представлен в виде нескольких звеньев.

По направлению прохождения воздействия различают вход и выход и соответственно входную и выходную величины звена. Выходная величина звена направленного действия не оказывает влияния на входную величину. Дифференциальные уравнения таких звеньев можно составлять отдельно и независимо от других звеньев. Поскольку в САУ входят различные усилители, обладающие направленным действием, САУ обладает способностью передавать воздействия только в одном направлении. Поэтому уравнение динамики всей системы можно получить из уравнений динамики ее звеньев, исключая промежуточные переменные.

Элементарные динамические звенья являются основой для построения математической модели системы любой сложности.

Классификация и динамические характеристики звеньев

Тип звена определяется алгоритмом, в соответствии с которым происходит преобразование входного воздействия. В зависимости от алгоритма различают следующие типы элементарных динамических звеньев: пропорциональное (усилительное), апериодическое (инерционное), колебательное, интегрирующее и дифференцирующее.

Каждое звено характеризуется следующими динамическими характеристиками: уравнением динамики (движения), передаточной функцией, переходной и импульсной переходной (весовой) функциями, частотными характеристиками. Такими же динамическими характеристиками оцениваются и свойства автоматической системы. Рассмотрим динамические характеристики на примере апериодического звена,

Рис. 2.2. Электрическая -цепь, представляемая апериодическим звеном, и реакции звена на типовые входные воздействия: а - схема; б - единичное ступенчатое воздействие; в - переходная функция звена; - единичный импульс; д - импульсная переходная функция звена.

которым представляется электрическая цепь, изображенная на рис. 2.2, а.

Уравнение динамики звена (системы). Уравнение динамики элемента (звена) - уравнение, определяющее зависимость выходной величины элемента (звена) от входной величины

Уравнение динамики можно записать в дифференциальной и операционной формах. Для получения дифференциального уравнения элемента составляются дифференциальные уравнения для входной и выходной величин этого элемента. Применительно к электрической цепи (рис. 2.2, а):

Дифференциальное уравнение цепи получают из этих уравнений исключением промежуточной переменной

где - постоянная времени, с; - коэффициент усиления звена.

В теории автоматического управления принята следующая форма записи уравнения: выходная величина и ее производные находятся в левой части, причем на первом месте стоит производная высшего порядка; выходная величина входит в уравнение с коэффициентом, равным единице; входная величина, а также в более общем случае ее производные и другие члены (возмущения) стоят в правой части уравнения. Уравнение (2.1) записано в соответствии с этой формой.

Элемент системы, процесс в котором описывается уравнением вида (2.1), представляется апериодическим звеном (инерционным, статическим звеном первого порядка).

Для получения уравнения динамики в операционной (по Лапласу) форме функции, входящие в дифференциальное уравнение, заменяются преобразованными по Лапласу функциями, а операции дифференцирования

и интегрирования в случае нулевых начальных условий - умножением и делением на комплексную переменную изображений функций, от которых берется производная или интеграл. В результате этого осуществляется переход от дифференциального уравнения к алгебраическому. В соответствии с дифференциальным уравнением (2.1) уравнение динамики апериодического звена в операционной форме для случая нулевых начальных условий имеет вид:

где - изображение по Лапласу функции времени - комплексное число.

Не следует путать операционную форму (2.2) записи уравнения с символической формой записи дифференциального уравнения:

где - символ дифференцирования. Отличить символ «дифференцирования от комплексной переменной несложно: после символа дифференцирования стоит оригинал, т. е. функция от а после комплексной переменной - изображение по Лапласу, т.е. функция от

Из формулы (2.1) видно, что апериодическое звено описывается уравнением первого порядка. Другие элементарные звенья описываются уравнениями нулевого, первого и максимум второго порядка.

Передаточная функция звена (системы) представляет собой отношение изображений по Лапласу выходной Хкых и входной величин при нулевых начальных условиях:

Передаточная функция звена (системы) может быть определена из уравнения звена (системы), записанного в операционной форме. Для апериодического звена в соответствии с уравнением (2.2)

Из выражения (2.3) следует

т. е. зная изображение по Лапласу входного воздействия и передаточную функцию звена (системы), можно определить изображение выходной величины этого звена (системы).

Изображение выходной величины апериодического звена в соответствии с выражением (2.4) следующее:

Переходной функцией звена (системы) h(t) называется реакция звена (системы) на воздействие вида единичной ступенчатой функции (рис. 2.2, б) при нулевых начальных условиях. Переходная функция может быть определена решением дифференциального уравнения обычным или операционным методами. Для определения

операционным методом в уравнение (2.5) подставляем изображение единичной ступенчатой функции и находим изображение переходной функции

т. е. изображение переходной функции равно передаточной функции, деленной на Переходная функция находится как обратное преобразование Лапласа от

Для определения апериодического звена в уравнение (2.6) подставляем и находим изображение переходной функции

Разлагаем на алементарные дроби где и с помощью таблиц преобразования Лапласа находим оригинал

График переходной функции апериодического звена изображен на рис. 2.2, в. Из рисунка видно, что переходный процесс звена имеет апериодический характер. Выходная величина звена достигает своего значения не сразу, а постепенно. В частности, значение достигается через .

Импульсная переходная функция (весовая функция) звена (системы) есть реакция звена (системы) на единичный импульс (мгновенный импульс с бесконечно большой амплитудой и единичной площадью, рис. 2.2, г). Единичный импульс получается дифференцированием единичного скачка: или в операционной форме: Поэтому

т. е. изображение импульсной переходной функции равно передаточной функции звена (системы). Отсюда следует, что для характеристики динамических свойств звена (системы) в равной мере могут быть использованы как передаточная функция, так и импульсная переходная функция. Как видно из (2.8), чтобы получить импульсную переходную функцию, надо найти оригинал, соответствующий передаточной функции Импульсная переходная функция апериодического звена

В соответствии с (2.7) или при переходе к оригиналам импульсная переходная функция звена (системы) может быть также получена дифференцированием переходной функции. Импульсная переходная функция апериодического

(кликните для просмотра скана)

Рис. 2.3. Принципиальные схемы элементов, представляемых пропорциональным звеном: а - делитель напряжения; б - потенциометр; в - усилитель на транзисторе; г - редуктор.

Как видим, выражения (2.9) и (2.10) для совпадают. График импульсной переходной функции апериодического звена изображен на рис. 2.2, д.

Из выражения (2.5) и рассмотренных примеров следует, что при заданном входном воздействии выходная величина определяется передаточной функцией. Поэтому технические требования к выходной величине звена (системы) можно выразить через соответствующие требования к передаточной функции этого звена (системы). В теории автоматического управления метод исследования и проектирования систем с помощью передаточной функции является одним из основных методов.

Пропорциональное (усилительное) звено. Уравнение звена имеет вид:

т. е. между выходной и входной величинами звена имеется пропорциональная зависимость. Уравнение (2.11) в операционной форме

Из уравнения (2.12) определяется передаточная функция звена

т. е. передаточная функция пропорционального звена численно равна коэффициенту усиления. Примерами такого звена могут служить делитель напряжения, потенциометрический датчик, электронный усилительный каскад, идеальный редуктор, схемы которых изображены на рис. 2.3, а, б, е, г соответственно. Коэффициент усиления пропорционального звена может быть как безразмерной (делитель напряжения, усилительный каскад, редуктор), так и размерной величиной (потенциометрический датчик).

Оценим динамические свойства пропорционального звена. При подаче на вход звена ступенчатой функции выходная величина (переходная функция) в силу равенства (2.11) также будет ступенчатой (табл. 2.1), т. е. выходная величина копирует изменение входной

величины без запаздывания и искажения. Поэтому пропорциональное звено называют еще безынерционным.

Импульсная переходная функция пропорционального звена

т. e. представляет собой мгновенный бесконечно большой амплитуды импульс, площадь которого

Колебательное звено. Уравнение звена:

или в операционной форме

Тогда передаточная функция колебательного звена имеет вид

Динамические свойства звена зависят от корней его характеристического уравнения

Свободная составляющая решения

Полное решение уравнения (2.14) при ступенчатом входном воздействии (переходная функция звена) имеет вид:

где - угловая частота собственных колебаний; - начальная фаза колебаний; - декремент затухания; - относительный коэффициент затухания.

Что такое динамическое звено? На предыдущих занятиях мы рассматривали отдельные части системы автоматического управления и называли их элементами системы автоматического управления. Элементы могут иметь различный физический вид и конструктивное оформление. Главное, что на такие элементы подается некоторый входной сигнал х( t ) , и как отклик на этот входной сигнал, элемент системы управления формирует некоторый выходной сигнал у( t ) . Далее мы установили, что связь между выходным и входным сигналами определяется динамическими свойствами элемента управления, которые можно представить в виде передаточной функции W(s). Так вот, динамическим звеном называется любой элемент системы автоматического управления, имеющий определенное математическое описание, т.е. для которого известна передаточная функция.

Рис. 3.4. Элемент (а) и динамическое звено (б) САУ.

Типовые динамические звенья – это минимально необходимый набор звеньев для описания системы управления произвольного вида. К типовым звеньям относятся:

пропорциональное звено;

апериодическое звено I-ого порядка;

апериодическое звено II-ого порядка;

колебательное звено;

интегрирующее звено;

идеальное дифференцирующее звено;

форсирующее звено I-ого порядка;

форсирующее звено II-ого порядка;

звено с чистым запаздыванием.

Пропорциональное звено

Пропорциональное звено иначе еще называется безынерционным .

1. Передаточная функция.

Передаточная функция пропорционального звена имеет вид:

W (s ) = K где К – коэффициент усиления.

Пропорциональное звено описывается алгебраическим уравнением:

у(t ) = K · х(t )

Примерами таких пропорциональных звеньев могут служить, рычажный механизм, жесткая механическая передача, редуктор, электронный усилитель сигналов на низких частотах, делитель напряжения и др.

4. Переходная функция .

Переходная функция пропорциональное звена имеет вид:

h(t) = L -1 = L -1 = K · 1(t)

5. Весовая функция.

Весовая функция пропорционального звена равна:

w(t) = L -1 = K ·δ(t)

Рис. 3.5. Переходная функция, весовая функция, АФЧХ и АЧХ пропорционального звена.

6. Частотные характеристики .

Найдем АФЧХ, АЧХ, ФЧХ и ЛАХ пропорционального звена:

W(j ω ) = K = K +0 ·j

A(ω ) =
= K

φ(ω) = arctg(0/K) = 0

L(ω) = 20·lg = 20·lg(K)

Как следует из представленных результатов, амплитуда выходного сигнала не зависит от частоты. В действительности ни одно звено не в состоянии равномерно пропускать все частоты от 0 до ¥, как правило на высоких частотах, коэффициент усиления становится меньше и стремиться к нулю при ω → ∞. Таким образом, математическая модель пропорционального звена является некоторой идеализацией реальных звеньев .

Апериодическое звено I -ого порядка

Апериодические звенья иначе еще называются инерционными .

1. Передаточная функция.

Передаточная функция апериодического звена I-ого порядка имеет вид:

W (s ) = K /(T · s + 1)

где K – коэффициент усиления; T – постоянная времени, характеризующая инерционность системы, т.е. продолжительность переходного процесса в ней. Поскольку постоянная времени характеризует некоторый временной интервал , то ее величина должна быть всегда положительной, т.е. (T > 0).

2. Математическое описание звена.

Апериодическое звено I-ого порядка описывается дифференциальным уравнением первого порядка:

T · d у(t )/ dt + у(t ) = K ·х(t )

3. Физическая реализация звена.

Примерами апериодического звена I-ого порядка могут служить: электрический RC-фильтр; термоэлектрический преобразователь; резервуар с сжатым газом и т.п.

4. Переходная функция .

Переходная функция апериодического звена I-ого порядка имеет вид:

h(t) = L -1 = L -1 = K – K·e -t/T = K·(1 – e -t/T )

Рис. 3.6. Переходная характеристика апериодического звена I-го порядка.

Переходный процесс апериодического звена I-ого порядка имеет экспоненциальный вид. Установившееся значение равно: h уст = K. Касательная в точке t = 0 пересекает линию установившегося значения в точке t = T. В момент времени t = T переходная функция принимает значение: h(T) ≈ 0.632·K, т.е. за время T переходная характеристика набирает только около 63% от установившегося значения.

Определим время регулирования T у для апериодического звена I-ого порядка. Как известно из предыдущей лекции, время регулирования – это время, после которого разница между текущим и установившимся значениями не будет превышать некоторой заданной малой величины Δ. (Как правило, Δ задается как 5 % от установившегося значения).

h(T у) = (1 – Δ)·h уст = (1 – Δ)·K = K·(1 – e - T у/ T), отсюда е - T у/ T = Δ, тогда T у /T = -ln(Δ), В итоге получаем T у = [-ln(Δ)]·T.

При Δ = 0,05 T у = - ln(0.05)·T ≈ 3·T.

Другими словами, время переходного процесса апериодического звена I-ого порядка приблизительно в 3 раза превышает постоянную времени.

Алгоритмические звенья, которые описываются обыкновенными дифференциальными уравнениями первого и второго порядка, получили название типовых динамических звеньев .

Типовые динамические звенья являются основными составными частями алгоритмических структур непрерывных систем управления, знание их характеристик существенно облегчает анализ таких систем.

Классификацию удобно осуществить, рассматривая различные частные формы дифференциального уравнения:

наименование примечания Безынерционное (пропорциональное) Статическое элементарное Инерционное первого порядка (апериодическое) Статическое инерционное Инерционное второго порядка (апериодическое) Т 1 2Т 2 Статическое инерционное Инерционное второго порядка (колебательное) Статическое инерционное Идеальное интегрирующее элементарное Реальное интегрирующее инерционное Идеальное дифференцирующее элементарное Реальное дифференцирующее инерционное Изодромное (пропорционально- интегрирующее) Форсирующее (пропорционально- дифференцирующее) Статическое Упругое (интегро- дифференцирующее, реально-форсирующее) -преобладают интегрирующие свойства -преобладают дифференцирующие свойства Статическое, инерционное

Звенья, у которых а 2 0 и в 1 0 обладают статизмом, т.е. однозначной связью между входной и выходной переменными в статическом режиме. Звенья – статические, или позиционные.

Звенья, у которых 2 из трех коэффициентов а 2 0, а 1 0, а 0 0, обладают инерционностью (замедлением).

У звеньев 1,5,7 только 2 коэффициента 0. Они являются простейшими, или элементарными. Все остальные типовые звенья могут быть образованы из элементарных путем последовательного, параллельного и встречно- параллельного соединения.

Апериодическое звено

Динамика процесса описывается следующим уравнением:

где k  передаточный коэффициент или коэффициент усиления, Т  постоянная времени, характеризующая инерционность звена.

1. Переходная характеристика:

1)

2) В точке ноль строят касательную переходной характеристики, определяют точку пересечения с линией k . Абсцисса этой точки и есть постоянная времени.

2. Импульсная переходная характеристика, или функция веса, звена может быть получена путем дифференцирования функции h (t ) :

3. Передаточная функция:

П

рименим преобразование Лапласа к уравнению:

Структурная схема звена при этом будет выглядеть следующим образом:

Подставляя в передаточную функцию p = j  , получим амплитудно-фазо-частотную функцию:

5. АЧХ:

График АЧХ строится по точкам:

Здесь  с – частота сопряжения.

Гармонические сигналы малой частоты ( <  с ) пропускаются звеном хорошо – с отношением амплитуд выходной и входной величин, близким к передаточному коэффициенту k . Сигналы большой частоты ( >  с ) плохо пропускаются звеном: отношение амплитуд существенно < коэффициента k . Чем больше постоянная времени Т , т.е. чем больше инерционность звена, тем меньше АЧХ вытянута вдоль оси частот, или, тем у же полоса пропускания частот.

Т.о. инерционное звено первого порядка по своим частотным свойствам является фильтром низкой частоты .

ФЧХ инерционного звена первого порядка равна:

Чем больше частота входного сигнала, тем больше отставание по фазе выходной величины от входной. Максимально возможное отставание равно 90 0 . При частоте  с = 1/Т сдвиг фаз равен –45 0 .

Рассмотрим теперь ЛАЧХ звена. Точная ЛАЧХ описывается выражением:

При построении ЛАЧХ апериодического звена прибегают к асимптотическим методам или, другими словами, строят асимптотический график ЛАЧХ.

Значение сопрягающей частоты w c , при которой пересекаются обе асимптоты, найдем из условия

Посмотрим, что будет при построении не асимптотической, а точной ЛАЧХ:

Точная характеристика (ЛАЧХ) в точке среза будет меньше асимптотической ЛАЧХ на величину
.

Существует так называемое неустойчивое апериодическое звено

Колебательное звено

Динамика процессов в колебательном звене описывается уравнением:

,

где k  коэффициент усиления звена; Т  постоянная времени колебательного звена;  коэффициент демпфирования звена (или коэффициент затухания).

В зависимости от величины коэффициента демпфирования различают четыре типа звеньев:

а) колебательное 0<<1;

б) апериодическое звено II порядка>1;

в) консервативное звено =0;

г) неустойчивое колебательное звено <0.

1. Переходная характеристика колебательного звена:

А

мплитуды первых двух колебаний определяют величину
, или её можно найти, определив постоянную времени экспоненты, с которой происходит затухание

Чем ближе коэффициент затухания к единице, тем меньше амплитуда колебаний, чем меньше Т , тем быстрее устанавливаются переходные процессы.

При  >1 колебательное звено называется апериодическим звеном второго порядка (последовательное соединение двух апериодических звеньев с постоянными времени Т 1 и Т 2 ).

, или можно записать так
.

Здесь  0 – величина, обратная постоянной времени (
);
.

Такое звено в литературе называют консервативным звеном .

Все переходные характеристики будут колебаться вдоль величины k .

2. Импульсная переходная характеристика:

3

.Передаточная функция:

График АФЧХ будет выглядеть следующим образом:

Это характеристика для колебательного звена и для апериодического звена второго порядка.

Для апериодического звена -
.

-

АФЧХ для консервативного звена.

.

А

ЧХ при частоте
имеет максимум (резонансный пик), равный

Отсюда видно, что, чем меньше коэффициент  , тем больше резонансный пик.

Т

.о., по графику АЧХ видно, что колебательное звено, как и все инерционные звенья, хорошо пропускает сигналы низкой частоты и плохо – сигналы высокой частоты; если частота гармонического входного сигнала близка к частоте собственных колебаний звена, то отношение амплитуды выходного сигнала к амплитуде входного больше передаточного коэффициента k .

Для случая б) график будет аналогичным, только перегиб будет чуть меньше (штриховая линия на графике).

Где

Асимптотическая ЛАЧХ колебательного звена:

Определяем наклон на втором участке:

Шаблон к графику а) дается от 0 до 1 шагом в 0,1.

К

онсервативное звено:

Структурная схема колебательного звена будет выглядеть следующим образом:

Примером колебательного звена является любая RLС- цепь.

Общие свойства статических звеньев

В установившемся режиме выходная переменная y однозначно связана с входной переменной x уравнением статики

Передаточный коэффициент звена связан с передаточной функцией соотношением

Звенья являются звеньями низкой частоты (кроме безынерционного), т.е. хорошо пропускают низкочастотные сигналы и плохо – высокочастотные, в режиме гармонических колебаний создают отрицательные фазовые сдвиги.