На практическом занятии мы повторим основные типы заданий из темы «Тригонометрия», дополнительно разберем задачи повышенной сложности и рассмотрим примеры решения различных тригонометрических неравенств и их систем.
Данный урок поможет Вам подготовиться к одному из типов заданий В5, В7, С1 и С3.
Начнем с повторения основных типов заданий, которые мы рассмотрели в теме «Тригонометрия» и решим несколько нестандартных задач.
Задача №1 . Выполнить перевод углов в радианы и градусы: а) ; б) .
а) Воспользуемся формулой перевода градусов в радианы
Подставим в нее указанное значение .
б) Применим формулу перевода радиан в градусы
Выполним подстановку 
.
Ответ. а) ; б) .
Задача №2 . Вычислить: а) ; б) .
а) Поскольку угол далеко выходит за рамки табличного, уменьшим его с помощью вычитания периода синуса. Т.к. угол указан в радианах, то и период будем рассматривать как .
б) В данном случае ситуация аналогичная. Поскольку угол указан в градусах, то и период тангенса будем рассматривать как .
Полученный угол хоть и меньше периода, но больше , а это значит, что он относится уже не к основной, а к расширенной части таблицы. Чтобы не тренировать лишний раз свою память запоминанием расширенной таблицы значений тригофункций, вычтем период тангенса еще раз:
Воспользовались нечетностью функции тангенс.
Ответ. а) 1; б) .
Задача №3
. Вычислить 
, если .
Приведем все выражение к тангенсам, разделив числитель и знаменатель дроби на . При этом, можем не бояться, что , т.к. в таком случае значения тангенса не существовало бы.
Задача №4 . Упростить выражение .
Указанные выражения преобразовываются с помощью формул приведения. Просто они непривычно записаны с использованием градусов. Первое выражение вообще представляет собой число. Упростим все тригофункции по очереди:
Т.к. , то функция меняется на кофункцию, т.е. на котангенс, и угол попадает во вторую четверть, в которой у исходного тангенса знак отрицательный.
По тем же причинам, что и предыдущем выражении, функция меняется на кофункцию, т.е. на котангенс, а угол попадает в первую четверть, в которой у исходного тангенса знак положительный.
Подставим все в упрощаемое выражение:
Задача №5 . Упростить выражение .
Распишем тангенс двойного угла по соответствующей формуле и упростим выражение:
Последнее тождество является одной из формул универсальной замены для косинуса.
Задача №6 . Вычислить .
Главное, это не сделать стандартной ошибки и не дать ответ, что выражение равно . Воспользоваться основным свойством арктангенса нельзя пока возле него присутствует множитель в виде двойки. Чтобы от него избавиться распишем выражение по формуле тангенса двойного угла , при этом относимся к , как к обыкновенному аргументу.
Теперь уже можно применять основное свойство арктангенса, вспомним, что на его численный результат ограничений нет.
Задача №7 . Решить уравнение .
При решении дробного уравнения, которое приравнивается к нулю, всегда указывается, что числитель равен нулю, а знаменатель нет, т.к. на ноль делить нельзя.
Первое уравнение представляет собой частный случай простейшего уравнения, которое решается с помощью тригонометрической окружности. Вспомните самостоятельно этот способ решения. Второе неравенство решается как простейшее уравнение по общей формуле корней тангенса, но только с записью знака неравно.
Как видим, одно семейство корней исключает другое точно такое же по виду семейство не удовлетворяющих уравнению корней. Т.е. корней нет.
Ответ. Корней нет.
Задача №8 . Решить уравнение .
Сразу заметим, что можно вынести общий множитель и проделаем это:
Уравнение свелось к одной из стандартных форм, когда произведение нескольких множителей равно нулю. Мы уже знаем, что в таком случае или один из них равен нулю или другой, или третий. Запишем это в виде совокупности уравнений:
Первые два уравнения являются частными случаями простейших, с подобными уравнениями мы уже многократно встречались, поэтому сразу укажем их решения. Третье уравнение приведем к одной функции с помощью формулы синуса двойного угла.
Решим отдельно последнее уравнение:
Данное уравнение не имеет корней, т.к. значение синуса не могут выходить за пределы 
.
Таким образом, решением является только два первых семейства корней, их можно объединить в одно, что легко показать на тригонометрической окружности:
 |
Это семейство всех половин , т.е.
Перейдем к решению тригонометрических неравенств. Сначала разберем подход к решению примера без использования формул общих решений, а с помощью тригонометрической окружности.
Задача №9 . Решить неравенство .
Изобразим на тригонометрической окружности вспомогательную линию, соответствующую значению синуса равному , и покажем промежуток углов, удовлетворяющих неравенству.
 |
Очень важно понять, как именно указывать полученный промежуток углов, т.е. что является его началом, а что концом. Началом промежутка будет угол, соответствующей точке, в которую мы войдем в самом начале промежутка, если будем двигаться против часовой стрелки. В нашем случае это точка, которая находится слева, т.к. двигаясь против часовой стрелки и проходя правую точку, мы наоборот выходим из необходимого промежутка углов. Правая точка будет, следовательно, соответствовать концу промежутка.
Теперь необходимо понять значения углов начала и конца нашего промежутка решений неравенства. Типичная ошибка - это указать сразу, что правой точке соответствует угол , левой и дать ответ . Это неверно! Обратите внимание, что мы только что указали промежуток, соответствующий верхней части окружности, хотя нас интересует нижняя, иными словами, мы перепутали начало и конец необходимого нам интервала решений.
Чтобы интервал начинался с угла правой точки, а заканчивался углом левой точки, необходимо, чтобы первый указанный угол был меньше второго. Для этого угол правой точки нам придется отмерять в отрицательном направлении отсчета, т.е. по часовой стрелке и он будет равен . Тогда, начиная движение с него в положительном направлении по часовой стрелке, мы попадем в правую точку уже после левой точки и получим для нее значение угла . Теперь начало промежутка углов меньше конца , и мы можем записать промежуток решений без учета периода:
Учитывая, что такие промежутки будут повторяться бесконечное количество раз после любого целого количества поворотов, получим общее решение с учетом периода синуса :
Круглые скобки ставим из-за того, что неравенство строгое, и точки на окружности, которые соответствуют концам промежутка, мы выкалываем.
Сравните полученный ответ с формулой общего решения, которую мы приводили на лекции.
Ответ.
.
Указанный способ хорош для понимания того, откуда берутся формулы общих решений простейших тригонеравенств. Кроме того, он полезен для тех, кому лень учить все эти громоздкие формулы. Однако сам по себе способ тоже непростой, выберете, какой подход к решению вам наиболее удобен.
Для решения тригонометрических неравенств можно использовать и графики функций, на которых строится вспомогательная линия аналогично показанному способу с использованием единичной окружности. Если вам интересно, попробуйте самостоятельно разобраться с таким подходом к решению. В дальнейшем будем использовать общие формулы для решения простейших тригонометрических неравенств.
Задача №10 . Решить неравенство .
Воспользуемся формулой общего решения с учетом того, что неравенство нестрогое:
Получаем в нашем случае:
Ответ. 
Задача №11 . Решить неравенство .
Воспользуемся формулой общего решения для соответствующего строго неравенства:
Ответ.
.
Задача №12 . Решить неравенства: а) ; б) .
В указанных неравенствах не надо спешить использовать формулы общих решений или тригонометрическую окружность, достаточно просто вспомнить об области значений синуса и косинуса.
а) Поскольку 
, то неравенство не имеет смысла. Следовательно, решений нет.
б) Т.к. аналогично , то синус от любого аргумента всегда удовлетворяет указанному в условии неравенству . Следовательно неравенству удовлетворяют все действительные значения аргумента .
Ответ. а) решений нет; б) .
Задача 13
. Решить неравенство 
.
Министерство образования Республики Беларусь
Учреждение образования
«Гомельский государственный университет
имени Франциска Скорины»
Математический факультет
Кафедра алгебры и геометрии
Допущена к защите
Зав. кафедройШеметков Л.А.
Тригонометрические уравнения и неравенства
Курсовая работа
Исполнитель:
студент группы М-51
С.М. Горский
Научный руководительк.ф.- м.н.,
старший преподаватель
В.Г. Сафонов
Гомель 2008
ВВЕДЕНИЕ
ОСНОВНЫЕ МЕТОДЫ РЕШЕНИЯ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ
Разложение на множители
Решение уравнений преобразованием произведения тригонометрических функций в сумму
Решение уравнений с применением формул тройного аргумента
Домножение на некоторую тригонометрическую функцию
НЕСТАНДАРТНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ
ТРИГОНОМЕТРИЧЕСКИЕ НЕРАВЕНСТВА
ОТБОР КОРНЕЙ
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
ЗАКЛЮЧЕНИЕ
СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ
В древности тригонометрия возникла в связи с потребностями астрономии, землемерия и строительного дела, то есть носила чисто геометрический характер и представляла главным образом <<исчисление хорд>>. Со временем в нее начали вкрапляться некоторые аналитические моменты. В первой половине 18-го века произошел резкий перелом, после чего тригонометрия приняла новое направление и сместилась в сторону математического анализа. Именно в это время тригонометрические зависимости стали рассматриваться как функции.
Тригонометрические уравнения одна из самых сложных тем в школьном курсе математики. Тригонометрические уравнения возникают при решении задач по планиметрии, стереометрии, астрономии, физики и в других областях. Тригонометрические уравнения и неравенства из года в год встречаются среди заданий централизованного тестирования.
Самое важное отличие тригонометрических уравнений от алгебраических состоит в том, что в алгебраических уравнениях конечное число корней, а в тригонометрических --- бесконечное, что сильно усложняет отбор корней. Еще одной спецификой тригонометрических уравнений является неединственность формы записи ответа.
Данная дипломная работа посвящена методам решения тригонометрических уравнений и неравенств.
Дипломная работа состоит из 6 разделов.
В первом разделе приведены основные теоретические сведения: определение и свойства тригонометрических и обратных тригонометрических функций; таблица значений тригонометрических функций для некоторых аргументов; выражение тригонометрических функций через другие тригонометрических функции, что очень важно для преобразования тригонометрических выражений, в особенности содержащих обратные тригонометрические функции; кроме основных тригонометрических формул, хорошо известных из школьного курса, приведены формулы упрощающие выражения, содержащие обратные тригонометрические функции.
Во втором разделе изложены основные методы решения тригонометрических уравнений. Рассмотрены решение элементарных тригонометрических уравнений, метод разложения на множители, методы сведения тригонометрических уравнений к алгебраическим. Ввиду того, что решения тригонометрических уравнений можно записать несколькими способами, и вид этих решений не позволяет сразу установить, являются ли эти решения одинаковыми или различными, что может <<сбить с толку>> при решении тестов, рассмотрена общая схема решения тригонометрических уравнений и подробно рассмотрено преобразование групп общих решений тригонометрических уравнений.
В третьем разделе рассматриваются нестандартные тригонометрические уравнения, решения которых основано на функциональном подходе.
В четвертом разделе рассматриваются тригонометрические неравенства. Подробно рассмотрены методы решения элементарных тригонометрических неравенств, как на единичной окружности, так и графическим методом. Описан процесс решения неэлементарных тригонометрических неравенств через элементарные неравенства и уже хорошо известный школьникам метод интервалов.
В пятом разделе представлены наиболее сложные задания: когда необходимо не только решить тригонометрическое уравнение, но и из найденных корней отобрать корни, удовлетворяющие какому-нибудь условию. В данном разделе приведены решения типичных заданий на отбор корней. Приведены необходимые теоретических сведения для отбора корней: разбиение множества целых чисел на непересекающиеся подмножества, решение уравнений в целых числах (диафантовых).
В шестом разделе представлены задачи для самостоятельного решения, оформленные в виде теста. В 20 заданиях теста приведены наиболее сложные задания, которые могут встретиться на централизованном тестировании.
Элементарные тригонометрические уравнения
Элементарные тригонометрические уравнения --- это уравнения вида , где --- одна из тригонометрических функций: , , , .
Элементарные тригонометрические уравнения имеют бесконечно много корней. Например, уравнению удовлетворяют следующие значения: , , , и т. д. Общая формула по которой находятся все корни уравнения , где , такова:
Здесь может принимать любые целые значения, каждому из них соответствует определенный корень уравнения; в этой формуле (равно как и в других формулах, по которым решаются элементарные тригонометрические уравнения) называют параметром . Записывают обычно , подчеркивая тем самым, что параметр принимать любые целые значения.
Решения уравнения , где , находятся по формуле
Уравнение решается применяя формулу
а уравнение --- по формуле
Особо отметим некоторые частные случаи элементраных тригонометрических уравнений, когда решение может быть записано без применения общих формул:
При решении тригонометрических уравнений важную роль играет период тригонометрических функций. Поэтому приведем две полезные теоремы:
Теорема Если --- основной период функции , то число является основным периодом функции .
Периоды функций и называются соизмеримыми, если существуют натуральные числа и , что .
Теорема Если периодические функции и , имеют соизмеримые и , то они имеют общий период , который является периодом функций , , .
В теореме говорится о том, что является периодом функции , , , и не обязательно является основным периодом. Например, основной период функций и --- , а основной период их произведения --- .
Введение вспомогательного аргумента
Стандартным путем преобразования выражений вида 
является следующий прием: пусть --- угол, задаваемый равенствами 
, 
. Для любых и такой угол существует. Таким образом . Если , или , , , в других случаях .
Схема решения тригонометрических уравнений
Основная схема, которой мы будем руководствоваться при решении тригонометрических уравнений следующая:
решение заданного уравнения сводится к решению элементарных уравнений. Средства решения --- преобразования, разложения на множители, замена неизвестных. Ведущий принцип --- не терять корней. Это означает, что при переходе к следующему уравнению (уравнениям) мы не опасаемся появления лишних (посторонних) корней, а заботимся лишь о том, чтобы каждое последующее уравнение нашей "цепочки" (или совокупность уравнений в случае ветвления) являлось следствием предыдущего. Одним из возможных методов отбора корней является проверка. Сразу заметим, что в случае тригонометрических уравнений трудности, связанные с отбором корней, с проверкой, как правило, резко возрастают по сравнению с алгебраическими уравнениями. Ведь проверять приходится серии, состоящие из бесконечного числа членов.
Особо следует сказать о замене неизвестных при решении тригонометрических уравнений. В большинстве случаев после нужной замены получается алгебраическое уравнение. Более того, не так уж и редки уравнения, которые, хотя и являются тригонометрическими по внешнему виду, по существу таковыми не являются, поскольку уже после первого шага --- замены переменных --- превращаются в алгебраические, а возращение к тригонометрии происходит лишь на этапе решения элементарных тригонометрических уравнений.
Еще раз напомним: замену неизвестного следует делать при первой возможности, получившееся после замены уравнение необходимо решить до конца, включая этап отбора корней, а уж затем возвратится к первоначальному неизвестному.
Одна из особенностей тригонометрических уравнений заключается в том, что ответ во многих случаях может быть записан различными способами. Даже для решения уравнения 
ответ может быть записан следующим образом:
1) в виде двух серий: 
, , ;
2) в стандартной форме представляющей собой объединение указанных выше серий: , ;
3) поскольку 
, то ответ можно записать в виде 
, . (В дальнейшем наличие параметра , , или в записи ответа автоматически означает, что этот параметр принимает всевозможные целочисленные значения. Исключения будут оговариваться.)
Очевидно, что тремя перечисленными случаями не исчерпываются все возможности для записи ответа рассматриваемого уравнения (их бесконечно много).
Например, при справедливо равенство 
. Следовательно, в двух первых случаях, если , мы можем заменить на .
Обычно ответ записывается на основании пункта 2. Полезно запомнить следующую рекомендацию: если на решении уравнения работа не заканчивается, необходимо еще провести исследование, отбор корней, то наиболее удобна форма записи, указанная в пункте 1. (Аналогичную рекомендацию следует дать и для уравнения .)
Рассмотрим пример иллюстрирующий сказанное.
Пример Решить уравнение .
Решение. Наиболее очевидным является следующий путь. Данное уравнение распадается на два: и . Решая каждое из них и объединяя полученные ответы, найдем .
Другой путь.
Поскольку , то, заменяя и по формулам понижения степени. После небольших преобразований получим , откуда 
.
На первый взгляд никаких особых преимуществ у второй формулы по сравнению с первой нет. Однако, если возьмем, например, , то окажется, что , т.е. уравнение имеет решение , в то время как первый способ нас приводит к ответу 
. "Увидеть" и доказать равенство 
не так просто.
Ответ. .
Преобразование и объединение групп общих решений тригонометрических уравнений
Будем рассматривать арифметическую прогрессию, бесконечно простирающуюся в обе стороны. Члены этой прогресссии можно разбить на две группы членов, располагающиеся вправо и влево от некоторого члена, называемого центральным или нулевым членом прогрессии.
Фиксируя один из членов бесконечной прогрессиии нулевым номером, мы должны будем вести двойную нумерацию для всех оставшихся членов: положительную для членов, расположенных вправо, и отрицательную для членов, расположенных влево от нулевого.
В общем случае, если разность прогрессии , нулевой член , формула для любого (-го) члена бесконечной арифметической прогрессии представляет вид:
Преобразования формулы для любого члена бесконечной арифметической прогрессии
1. Если к нулевому члену прибавить или отнять разность прогрессии , то от этого прогрессия не изменится, а только переместится нулевой член, т.е. изменится нумерация членов.
2. Если коэффициент при переменной величине умножить на , то от этого произойдет лишь перестановка правой и левой групп членов.
3. Если последовательных членов бесконечной прогрессии
например , , , ..., , сделать центральными членами прогрессий с одинаковой разностью, равной :
то прогрессия и ряд прогрессий выражают собой одни и те же числа.
Пример Ряд может быть заменен следующими тремя рядами: , , .
4. Если бесконечных прогрессий с одинаковой разностью имеют центральными членами числа, образующие арифметическую прогрессию с разностью , то эти рядов могут быть заменены одной прогрессией с разностью , и с центральным членом, равным любому из центральных членов данных прогрессий, т.е. если
то эти прогрессий объединяются в одну:
Пример
, , , обе объединяются в одну группу , так как 
.
Для преобразования групп, имеющих общие решения, в группы, общих решений не имеющие данные группы разлагают на группы с общим периодом, а затем стремяться объединить получившиеся группы, исключив повторяющиеся.
Разложение на множители
Метод разложения на множетели заключается в следующем: если
то всякое решение уравнения
является решение совокупности уравнений
Обратное утверждение, вообще говоря неверно: не всякое решение совокупности является решением уравнения. Это объясняется тем, что решения отдельных уравнений могут не входить в область определения функции .
Пример Решить уравнение .
Решение. Используя основное тригонометрическое тождество, уравнение представим в виде
Ответ.
; 
.
Преобразование суммы тригонометрических функций в произведение
Пример
Решить уравнение 
.
Решение. Применим формулу, получим равносильное уравнение
Ответ. .
Пример Решить уравнение .
Решение.
В данном случае, прежде чем применять формулы суммы тригонометрических функций, следует использовать формулу приведения 
. В итоге получим равносильное уравнение
Ответ.
, 
.
Решение уравнений приобразованием произведения тригонометрических функций в сумму
При решении ряда уравнений применяются формулы.
Пример Решить уравнение
Решение.
Ответ. , .
Пример Решить уравнение .
Решение. Применив формулу, получим равносильное уравнение:
Ответ. .
Решение уравнений с применением формул понижения степени
При решении широкого круга тригонометрических уравнений ключевую роль играют формулы.
Пример Решить уравнение .
Решение. Применяя формулу, получим равносильное уравнение.
Ответ. ; .
Решение уравнений с примененнием формул тройного аргумента
Пример Решить уравнение .
Решение. Применим формулу, получим уравнение
Ответ. ; .
Пример
Решить уравнение 
.
Решение.
Применим формулы понижения степени получим: 
. Применяя получаем:
Ответ. ; .
Равенство одноименных тригонометрических функций
Пример Решить уравнение .
Решение.
Ответ. , .
Пример
Решить уравнение 
.
Решение. Преобразуем уравнение.
Ответ. .
Пример Известно, что и удовлетворяют уравнению
Найти сумму .
Решение. Из уравнения следует, что
Ответ. .
Рассмотрим суммы вида
Данные суммы можно преобразовать в произведение, домножив и разделив их на , тогда получим
Указанный прием может быть использован при решении некоторых тригонометрических уравнений, однако следует иметь в виду, что в результате возможно появление посторонних корней. Приведем обобщение данных формул:
Пример Решить уравнение .
Решение. Видно, что множество является решением исходного уравнения. Поэтому умножение левой и правой части уравнения на не приведет к появлению лишних корней.
Имеем 
.
Ответ. ; .
Пример Решить уравнение .
Решение. Домножим левую и правую части уравнения на и применив формулы преобразования произведения тригонометрических функций в сумму, пролучим
Это уравнение равносильно совокупности двух уравнений и , откуда и .
Так как корни уравнения не являются корнями уравнения, то из полученных множеств решений следует исключить . Значит во множестве нужно исключить .
Ответ. и , .
Пример
Решить уравнение 
.
Решение. Преобразуем выражение :
Уравнение запишется в виде:
Ответ. .
Сведение тригонометрических уравнений к алгебраическим
Сводящиеся к квадратным
Если уравнение имеет вид
то замена приводит его к квадратному, поскольку 
() и.
Если вместо слагаемого будет , то нужная замена будет .
Уравнение
сводится к квадратному уравнению
представлением как 
. Легко проверить, что при которых , не являются корнями уравнения, и, сделав замену , уравнение сводится к квадратному.
Пример Решить уравнение .
Решение. Перенесем в левую часть, заменим ее на , и выразим через и .
После упрощений получим: . Разделим почленно на , сделаем замену :
Возвращаясь к , найдем 
.
Уравнения, однородные относительно ,
Рассмотрим уравнение вида
где , , , ..., , --- действительные числа. В каждом слагаемом левой части уравнения степени одночленов равны , т. е. сумма степеней синуса и косинуса одна и та же и равна . Такое уравнение называется однородным относительно и , а число называется показателем однородности .
Ясно, что если , то уравнение примет вид:
решениями которого являются значения , при которых , т. е. числа , . Второе уравнение, записанное в скобках также является однородным, но степени на 1 ниже.
Если же , то эти числа не являются корнями уравнения.
При получим: , и левая часть уравнения (1) принимает значение .
Итак, при , и , поэтому можно разделить обе части уравнения на . В результате получаем уравнение:
которое, подстановкой легко сводится к алгебраическому:
Однородные уравнения с показателем однородности 1. При имеем уравнение .
Если , то это уравнение равносильно уравнению , , откуда , .
Пример Решите уравнение .
Решение. Это уравнение однородное первой степени . Разделим обе его части на получим: , , , .
Ответ. .
Пример При получим однородное уравнение вида
Решение.
Если , тогда разделим обе части уравнения на , получим уравнение 
, которое подстановкой легко приводится к квадратному: 
. Если 
, то уравнение имеет действительные корни , . Исходное уравнение будет иметь две группы решений: , , .
Если 
, то уравнение не имеет решений.
Пример Решите уравнение .
Решение. Это уравнение однородное второй степени. Разделим обе чести уравнения на , получим: . Пусть , тогда , , . , , ; , , .
Ответ.
.
К уравнению вида сводится уравнение
Для этого достаточно воспользоваться тождеством 
В частности, уравнение сводится к однородному, если заменить на 
, тогда получим равносильное уравнение:
Пример Решите уравнение .
Решение. Преобразуем уравнение к однородному:
Разделим обе части уравнения на 
, получим уравнение:
Пусть , тогда приходим к квадратному уравнению: 
, , 
, 
, .
Ответ.
.
Пример Решите уравнение .
Решение. Возведем обе части уравнения в квадрат, учитывая, что они имеют положительные значения: , ,
Пусть , тогда получим 
, , .
Ответ. .
Уравнения, решаемые с помощью тождеств 
Полезно знать следующие формулы:
Пример Решить уравнение .
Решение. Используя, получаем
Ответ.
Предлагаем не сами формулы, а способ их вывода:
следовательно,
Аналогично, .
Пример
Решить уравнение 
.
Решение. Преобразуем выражение :
Уравнение запишется в виде:
Принимая , получаем . , . Следовательно
Ответ. .
Универсальная тригонометрическая подстановка
Тригонометрическое уравнение вида
где --- рациональная функция с помощью фомул -- , а так же с помощью формул -- можно свести к рациональному уравнению относительно аргументов , , , , после чего уравнение может быть сведено к алгебраическому рациональному уравнению относительно с помощью формул универсальной тригонометрической подстановки
Следует отметить, что применение формул может приводить к сужению ОДЗ исходного уравнения, поскольку не определен в точках , поэтому в таких случаях нужно проверять, являются ли углы , корнями исходного уравнения.
Пример Решить уравнение .
Решение. По условию задачи . Применив формулы и сделав замену , получим
откуда и, следовательно, .
Уравнения вида
Уравнения вида , где --- многочлен, решаются с помощью замен неизвестных
Пример Решить уравнение .
Решение. Сделав замену и учитывая, что , получим
откуда , . --- посторонний корень, т.к. . Корнями уравнения 
являются .
Использование ограниченности функций
В практике централизованного тестирования не так уж редко встречаются уравнения, решение которых основывается на ограниченности функций и . Например:
Пример Решить уравнение .
Решение. Поскольку , , то левая часть не превосходит и равна , если
Для нахождения значений , удовлетворяющих обоим уравнениям, поступим следующим образом. Решим одно из них, затем среди найденных значений отберем те, которые удовлетворяют и другому.
Начнем со второго: , . Тогда , 
.
Понятно, что лишь для четных будет .
Ответ. .
Другая идея реализуется при решении следующего уравнения:
Пример
Решить уравнение 
.
Решение.
Воспользуемся свойством показательной функции: , 
.
Сложив почленно эти неравенства будем иметь:
Следовательно левая часть данного уравнения равна тогда и только тогда, когда выполняются два равенства:
т. е. может принимать значения , , , а может принимать значения , .
Ответ. , .
Пример
Решить уравнение 
.
Решение.
, . Следовательно, 
.
Ответ. .
Пример Решить уравнение
Решение.
Обозначим , тогда из определения обратной тригонометрической функции имеем 
и 
.
Так как , то из уравнения следует неравенство , т.е. . Поскольку и , то и . Однако и поэтому .
Если и , то . Так как ранее было установлено, что , то .
Ответ. , .
Пример Решить уравнение
Решение. Областью допустимых значений уравнения являются .
Первоначально покажем, что функция
При любых может принимать только положительные значения.
Представим функцию следующим образом: .
Поскольку , то имеет место , т.е. 
.
Следовательно, для доказательства неравенства , необходимо показать, что 
. С этой целью возведем в куб обе части данного неравенства, тогда
Полученное численное неравенство свидетельствует о том, что . Если при этом еще учесть, что , то левая часть уравнения неотрицательна.
Рассмотрим теперь правую часть уравнения.
Так как 
, то
Однако известно, что 
. Отсюда следует, что , т.е. правая часть уравнения не превосходит . Ранее было доказано, что левая часть уравнения неотрицательна, поэтому равенство в может быть только в том случае, когда обе его части равны , а это возможно лишь при .
Ответ. .
Пример Решить уравнение
Решение.
Обозначим и 
. Применяя неравенство Коши-Буняковского, получаем . Отсюда следует, что 
. C другой стороны имеет место 
. Следовательно, уравнение не имеет корней.
Ответ. .
Пример Решить уравнение:
Решение. Перепишем уравнение в виде:
Ответ. .
Функциональные методы решения тригонометрических и комбинированных уравнений
Не всякое уравнение в результате преобразований может быть сведено к уравнению того или иного стандартного вида, для которого существует определенный метод решения. В таких случаях оказывается полезным использовать такие свойства функций и , как монотонность, ограниченность, четность, периодичность и др. Так, если одна из функций убывает, а вторая возрастает на промежутке , то при наличии у уравнения корня на этом промежутке, этот корень единственный, и тогда его, например, можно найти подбором. Если же функция ограничена сверху, причем , а функция ограничена снизу, причем , то уравнение равносильно системе уравнений
Пример Решить уравнение
Решение. Преобразуем исходное уравнение к виду
и решим его как квадратное относительно . Тогда получим,
Решим первое уравнение совокупности. Учтя ограниченность функции , приходим к выводу, что уравнение может иметь корень только на отрезке . На этом промежутке функция возрастает, а функция 
убывает. Следовательно, если это уравнение имеет корень, то он единственный. Подбором находим .
Ответ. .
Пример Решить уравнение
Решение.
Пусть , и 
, тогда исходное уравнение можно записать в виде функционального уравнения . Поскольку функция нечетная, то . В таком случае получаем уравнение .
Так как , и монотонна на , то уравнение равносильно уравнению , т.е. 
, которое имеет единственный корень .
Ответ. .
Пример
Решить уравнение 
.
Решение.
На основании теоремы о производной сложной функции ясно, что функция 
убывающая (функция убывающая, возрастающая, убывающая). Отсюда понятно, что функция 
определенная на , убывающая. Поэтому данное уравнение имеет не более одного корня. Так как 
, то
Ответ. .
Пример Решить уравнение .
Решение. Рассмотрим уравнение на трех промежутках.
а) Пусть . Тогда на этом множестве исходное уравнение равносильно уравнению . Которое на промежутке решений не имеет, т. к. 
, , а . На промежутке исходное уравнение так же не имеет корней, т. к. 
, а .
б) Пусть . Тогда на этом множестве исходное уравнение равносильно уравнению
корнями которого на промежутке являются числа , , , .
в) Пусть . Тогда на этом множестве исходное уравнение равносильно уравнению
Которое на промежутке решений не имеет, т. к. , а . На промежутке уравнение так же решений не имеет, т. к. , , а .
Ответ. , , , .
Метод симметрии
Метод симметрии удобно применять, когда в формулировке задания присуствует требование единственности решения уравнения, неравенства, системы и т.п. или точное указание числа решений. При этом следует обнаружить какую-либо симметрию заданных выражений.
Нужно также учитывать многообразие различных возможных видов симметрии.
Не менее важным является четкое соблюдение логических этапов в рассуждениях с симметрией.
Обычно симметрия позволяет установить лишь необходимые условия, а затем требуется проверка их достаточности.
Пример Найти все значения параметра , при которых уравнение имеет единственное решение.
Решение. Заметим, что и --- четные функции, поэтому левая часть уравнения есть четная функция.
Значит если --- решение уравнения, то есть также решение уравнения. Если --- единственное решение уравнения, то, необходимо , .
Отберем возможные значения , потребовав, чтобы было корнем уравнения.
Сразу же отметим, что другие значения не могут удовлетворять условию задачи.
Но пока не известно, все ли отобранные в действительности удовлетворяют условию задачи.
Достаточность.
1) , уравнение примет вид 
.
2) , уравнение примет вид:
Очевидно, что , для всех и 
. Следовательно, последнее уравнение равносильно системе:
Тем самым, мы доказали, что при , уравнение имеет единственное решение.
Ответ. .
Решение с исследованием функции
Пример Докажите, что все решения уравнения
Целые числа.
Решение. Основной период исходного уравнения равен . Поэтому сначала исследуем это уравнение на отрезке .
Преобразуем уравнение к виду:
При помощи микрокалькулятора получаем:
Если , то из предыдущих равенств получаем:
Решив полученное уравнение, получим: .
Выполненные вычисления представляют возможность предположить, что корнями уравнения, принадлежащими отрезку , являются , и .
Непосредственная проверка подтверждает эту гипотезу. Таким образом, доказано, что корнями уравнения являются только целые числа , .
Пример
Решите уравнение 
.
Решение. Найдём основной период уравнения. У функции основной период равен . Основной период функции равен . Наименьшее общее кратное чисел и равно . Поэтому основной период уравнения равен . Пусть .
Очевидно, является решением уравнения. На интервале . Функция отрицательна. Поэтому другие корни уравнения следует искать только на интервалаx и .
При помоши микрокалькулятора сначала найдем приближенные значения корней уравнения. Для этого составляем таблицу значений функции 
на интервалах и ; т. е. на интервалах и .
| 0 | 0 | 202,5 | 0,85355342 |
| 3 | -0,00080306 | 207 | 0,6893642 |
| 6 | -0,00119426 | 210 | 0,57635189 |
| 9 | -0,00261932 | 213 | 0,4614465 |
| 12 | -0,00448897 | 216 | 0,34549155 |
| 15 | -0,00667995 | 219 | 0,22934931 |
| 18 | -0,00903692 | 222 | 0,1138931 |
| 21 | -0,01137519 | 225 | 0,00000002 |
| 24 | -0,01312438 | 228 | -0,11145712 |
| 27 | -0,01512438 | 231 | -0,21961736 |
| 30 | -0,01604446 | 234 | -0,32363903 |
| 33 | -0,01597149 | 237 | -0,42270819 |
| 36 | -0,01462203 | 240 | -0,5160445 |
| 39 | -0,01170562 | 243 | -0,60290965 |
| 42 | -0,00692866 | 246 | -0,65261345 |
| 45 | 0,00000002 | 249 | -0,75452006 |
| 48 | 0,00936458 | 252 | -0,81805397 |
| 51 | 0,02143757 | 255 | -0,87270535 |
| 54 | 0,03647455 | 258 | -0,91803444 |
| 57 | 0,0547098 | 261 | -0,95367586 |
| 60 | 0,07635185 | 264 | -0,97934187 |
| 63 | 0,10157893 | 267 | -0,99482505 |
| 66 | 0,1305352 | 270 | -1 |
| 67,5 | 0,14644661 |
Из таблицы легко усматриваются следующие гипотезы: корнями уравнения, принадлежащими отрезку , являются числа: ; ; . Непосредственная проверка подтверждает эту гипотезу.
Ответ.
; 
; .
Решение тригонометрических неравенств с помощью единичной окружности
При решении тригонометрических неравенств вида , где --- одна из тригонометрических функций, удобно использовать тригонометрическую окружность для того, чтобы наиболее наглядно представить решения неравенства и записать ответ. Основным методом решения тригонометрических неравенств является сведение их к простейшим неравенствам типа . Разберём на примере, как решать такие неравенства.
Пример Решите неравенство .
Решение. Нарисуем тригонометрическую окружность и отметим на ней точки, для которых ордината превосходит .
Для решением данного неравенства будут . Ясно также, что если некоторое число будет отличаться от какого-нибудь числа из указанного интервала на , то также будет не меньше . Следовательно, к концам найденного отрезка решения нужно просто добавить . Окончательно, получаем, что решениями исходного неравенства будут все 
.
Ответ.
.
Для решения неравенств с тангенсом и котангенсом полезно понятие о линии тангенсов и котангенсов. Таковыми являются прямые и соответственно (на рисунке (1) и (2)), касающиеся тригонометрической окружности.
Легко заметить, что если построить луч с началом в начале координат, составляющий угол с положительным направлением оси абсцисс, то длина отрезка от точки до точки пересечения этого луча с линией тангенсов в точности равна тангенсу угла, который составляет этот луч с осью абсцисс. Аналогичное наблюдение имеет место и для котангенса.
Пример Решите неравенство .
Решение.
Обозначим , тогда неравенство примет вид простейшего: . Рассмотрим интервал длиной, равной наименьшему положительному периоду (НПП) тангенса. На этом отрезке с помощью линии тангенсов устанавливаем, что . Вспоминаем теперь, что необходимо добавить , поскольку НПП функции . Итак, 
. Возвращаясь к переменной , получаем, что .
Ответ.
.
Неравенства с обратными тригонометрическими функциями удобно решать с использованием графиков обратных тригонометрических функций. Покажем, как это делается на примере.
Решение тригонометрических неравенств графическим методом
Заметим, что если --- периодическая функция, то для решения неравенства необходимо найти его решения на отрезке, длина которого равна периоду функции . Все решения исходного неравенства будут состоять из найденных значений , а также всех , отличающихся от найденных на любое целое число периодов функции .
Рассмотрим решение неравенства ().
Поскольку , то при неравенство решений не имеет. Если , то множество решений неравенства --- множество всех действительных чисел.
Пусть . Функция синус имеет наименьший положительный период , поэтому неравенство можно решить сначала на отрезке длиной , например, на отрезке . Строим графики функций и (). задаются неравенствами вида: и, откуда,
В данной работе были рассмотрены методы решения тригонометрических уравнений и неравенств, как простейших, так и олимпиадного уровня. Были рассмотрены основные методы решения тригонометрических уравнений и неравенств, причем, как специфические --- характерные только для тригонометрических уравнений и неравенств,--- так и общие функциональные методы решения уравнений и неравенств, применительно к тригонометрическим уравнениям.
В дипломной работе приведены основные теоретические сведения: определение и свойства тригонометрических и обратных тригонометрических функций; выражение тригонометрических функций через другие тригонометрических функции, что очень важно для преобразования тригонометрических выражений, в особенности содержащих обратные тригонометрические функции; кроме основных тригонометрических формул, хорошо известных из школьного курса, приведены формулы упрощающие выражения, содержащие обратные тригонометрические функции. Рассмотрены решение элементарных тригонометрических уравнений, метод разложения на множители, методы сведения тригонометрических уравнений к алгебраическим. Ввиду того, что решения тригонометрических уравнений можно записать несколькими способами, и вид этих решений не позволяет сразу установить, являются ли эти решения одинаковыми или различными, рассмотрена общая схема решения тригонометрических уравнений и подробно рассмотрено преобразование групп общих решений тригонометрических уравнений. Подробно рассмотрены методы решения элементарных тригонометрических неравенств, как на единичной окружности, так и графическим методом. Описан процесс решения неэлементарных тригонометрических неравенств через элементарные неравенства и уже хорошо известный школьникам метод интервалов. Приведены решения типичных заданий на отбор корней. Приведены необходимые теоретических сведения для отбора корней: разбиение множества целых чисел на непересекающиеся подмножества, решение уравнений в целых числах (диафантовых).
Результаты данной дипломной работы могут быть использованы в качестве учебного материала при подготовке курсовых и дипломных работ, при составлении факультативов для школьников, так же работа может применяться при подготовке учащихся к вступительным экзаменам и централизованному тестированию.
Выгодский Я.Я., Справочник по элементарной математике. /Выгодский Я.Я. --- М.: Наука, 1970.
Игудисман О., Математика на устном экзамене/ Игудисман О. --- М.: Айрис пресс, Рольф, 2001.
Азаров А.И., уравнения/Азаров А.И., Гладун О.М., Федосенко В.С. --- Мн.: Тривиум, 1994.
Литвиненко В.Н., Практикум по элементарной математике / Литвиненко В.Н.--- М.: Просвещение, 1991.
Шарыгин И.Ф., Факультативный курс по математике: решение задач/ Шарыгин И.Ф., Голубев В.И. --- М.: Просвещение, 1991.
Бардушкин В., Тригонометрические уравнения. Отбор корней/В. Бардушкин, А. Прокофьев.// Математика, №12, 2005 с. 23--27.
Василевский А.Б., Задания для внеклассной работы по математике/Василевский А.Б. --- Мн.: Народная асвета. 1988. --- 176с.
Сапунов П. И., Преобразование и объединение групп общих решений тригонометрических уравнений/Сапунов П. И. // Математическое просвещение, выпуск №3, 1935.
Бородин П., Тригонометрия. Материалы вступительных экзаменов в МГУ[текст]/П.Бородин, В.Галкин, В.Панфёров, И.Сергеев, В.Тарасов // Математика №1, 2005 с. 36--48.
Самусенко А.В., Математика: Типичные ошибки абитуриентов: Справочное пособие/Самусенко А.В., Казаченок В.В.--- Мн.: Вышейшая школа, 1991.
Азаров А.И., Функциональный и графический методы решения экзаменационных задач/Азаров А.И., Барвенов С.А.,--- Мн.: Аверсэв, 2004.
ОПРЕДЕЛЕНИЕ
Тригонометрическими неравенствами называются неравенства, которые содержат переменную под знаком тригонометрической функции.
Решение тригонометрических неравенств
Решение тригонометрических неравенств зачастую сводится к решению простейших тригонометрических неравенств вида: \(\ \sin x a \), \(\ \cos x > a \), \(\ \operatorname{tg} x > a \), \(\ \operatorname{ctg} x > a \), \(\ \sin x \leq a \), \(\ \cos x \leq a \), \(\ \operatorname{tg} x \leq a \), \(\ \operatorname{ctg} x \leq a \), \(\ \sin x \geq a \), \(\ \cos \geq a \), \(\ \operatorname{tg} x \geq a \), \(\ \operatorname{tg} x \geq a \)
Решаются простейшие тригонометрические неравенства графически или с помощью единичной тригонометрической окружности.
По определению, синусом угла \(\ \alpha \) есть ординатой точки \(\ P_{\alpha}(x, y) \) единичного круга (рис. 1), а косинусом – абсцисса этой точки. Этот факт используется при решении простейших тригонометрических неравенств с косинусом и синусом с помощью единичного круга.
Примеры решения тригонометрических неравенств
Решить неравенство \(\ \sin x \leq \frac{\sqrt{3}}{2} \)
Поскольку \(\ \left|\frac{\sqrt{3}}{2}\right| , то это неравенство имеет решение и его можно решить двумя способами
Первый способ. Решим это неравенство графически. Для этого построим в одной системе координат график синуса \(\ y=\sin x \) (рис. 2) и прямой \(\ y=\frac{\sqrt{3}}{2} \)
Выделим промежутки, на которых синусоида расположена ниже графика прямой \(\ y=\frac{\sqrt{3}}{2} \) . Найдем абсциссы \(\ x_{1} \) и \(\ x_{2} \) точек пересечения этих графиков: \(\ x_{1}=\pi-\arcsin \frac{\sqrt{3}}{2}=\pi-\frac{\pi}{3}=\frac{2 \pi}{3} x_{2}=\arcsin \frac{\sqrt{3}}{2}+2 \pi=\frac{\pi}{3}+2 \pi=\frac{7 \pi}{3} \)
Получили интервал \(\ \left[-\frac{4 \pi}{3} ; \frac{\pi}{3}\right] \) но так как функцию \(\ y=\sin x \) периодическая и имеет период \(\ 2 \pi \) , то ответом будет объединение интервалов: \(\ \left[\frac{2 \pi}{3}+2 \pi k ; \frac{7 \pi}{3}+2 \pi k\right] \), \(\ k \in Z \)
Второй способ. Построим единичную окружность и прямую \(\ y=\frac{\sqrt{3}}{2} \) , точки их пересечения обозначим \(\ P_{x_{1}} \) и \(\ P_{x_{2}} \) (рис. 3). Решением исходного неравенства будет множество точек ординаты, которых меньше \(\ \frac{\sqrt{3}}{2} \) . Найдем значение \(\ \boldsymbol{I}_{1} \) и \(\ \boldsymbol{I}_{2} \) , совершая обход против часовой стрелки, \(\ x_{1} Рис. 3
\(\ x_{1}=\pi-\arcsin \frac{\sqrt{3}}{2}=\pi-\frac{\pi}{3}=\frac{2 \pi}{3} x_{2}=\arcsin \frac{\sqrt{3}}{2}+2 \pi=\frac{\pi}{3}+2 \pi=\frac{7 \pi}{3} \)
Учитывая периодичность функции синус, окончательно получим интервалы \(\ \left[\frac{2 \pi}{3}+2 \pi k ; \frac{7 \pi}{3}+2 \pi\right] \), \(\ k \in Z \)
Решить неравенство \(\ \sin x>2 \)
Синус – функция ограниченная: \(\ |\sin x| \leq 1 \) , а правая часть данного неравенства больше единицы, поэтому решений нет.
Решить неравенство \(\ \cos x>\frac{1}{2} \)
Данное неравенство можно решить двумя способами: графически и с помощью единичного круга. Рассмотрим каждый из способов.
Первый способ. Изобразим в одной системе координат функции, описывающие левую и правую части неравенства, то есть \(\ y=\cos x \) и \(\ y=\frac{1}{2} \) . Выделим промежутки, на которых график функции косинус \(\ y=\cos x \) расположен выше графика прямой \(\ y=\frac{1}{2} \) (рис. 4).
Найдем абсциссы точек \(\ \boldsymbol{x}_{1} \) и \(\ x_{2} \) – точек пересечения графиков функций \(\ y=\cos x \) и \(\ y=\frac{1}{2} \) , которые являются концами одного из промежутков, на котором выполняется указанное неравенство. \(\ x_{1}=-\arccos \frac{1}{2}=-\frac{\pi}{3} \); \(\ x_{1}=\arccos \frac{1}{2}=\frac{\pi}{3} \)
Учитывая, что косинус – функция периодическая, с периодом \(\ 2 \pi \) , ответом будет значения \(\ x \) из промежутков \(\ \left(-\frac{\pi}{3}+2 \pi k ; \frac{\pi}{3}+2 \pi k\right) \), \(\ k \in Z \)
Второй способ. Построим единичную окружность и прямую \(\ x=\frac{1}{2} \) (так как на единичной окружности косинусам отвечает ось абсцисс). Обозначим \(\ P_{x_{1}} \) и \(\ P_{x_{2}} \) (рис. 5) – точки пересечения прямой и единичной окружности. Решением исходного уравнения будет множество точек абсциссы, которых меньше \(\ \frac{1}{2} \) . Найдем значение \(\ x_{1} \) и \(\ 2 \) , совершая обход против часовой стрелки так, чтобы \(\ x_{1} Учитывая периодичность косинуса, окончательно получим интервалы \(\ \left(-\frac{\pi}{3}+2 \pi k ; \frac{\pi}{3}+2 \pi k\right) \),\(\ k \in Z \)
Решить неравенство \(\ \operatorname{ctg} x \leq-\frac{\sqrt{3}}{3} \)
Построим в одной системе координат графики функций \(\ y=\operatorname{ctg} x \), \(\ y=-\frac{\sqrt{3}}{3} \)
Выделим промежутки, на которых график функции \(\ y=\operatorname{ctg} x \) расположен не выше графика прямой \(\ y=-\frac{\sqrt{3}}{3} \) (рис. 6).
Найдем абсциссу точки \(\ x_{0} \) , которая является концом одного из промежутков, на котором неравенство \(\ x_{0}=\operatorname{arcctg}\left(-\frac{\sqrt{3}}{3}\right)=\pi-\operatorname{arcctg}\left(\frac{\sqrt{3}}{3}\right)=\pi-\frac{\pi}{3}=\frac{2 \pi}{3} \)
Другим концом этого промежутка есть точка \(\ \pi \) , а функция \(\ y=\operatorname{ctg} x \) в этой точке неопределенна. Таким образом, одним из решением данного неравенства является промежуток \(\ \frac{2 \pi}{3} \leq x
Тригонометрические неравенства со сложным аргументом
Тригонометрические неравенства со сложным аргументом можно свести к простейшим тригонометрическим неравенствам с помощью замены. После его решения делается обратная замена и выражается исходная неизвестная.
Решить неравенство \(\ 2 \cos \left(2 x+100^{\circ}\right) \leq-1 \)
Выразим в правой части данного неравенства косинус: \(\ \cos \left(2 x+100^{\circ}\right) \leq-\frac{1}{2} \)
Ведем замену \(\ t=2 x+100^{\circ} \) , после чего данное неравенство преобразуется к простейшему неравенству \(\ \cos t \leq-\frac{1}{2} \)
Решим его, используя единичную окружность. Построим единичный круг и прямую \(\ x=-\frac{1}{2} \) . Обозначим \(\ P_{1} \) и \(\ P_{2} \) – точки пересечения прямой и единичной окружности (рис. 7).
Решением исходного неравенства будет множество точек абсциссы, которых не больше \(\ -\frac{1}{2} \). Точке \(\ P_{1} \) соответствует угол \(\ 120^{\circ} \) , а точке \(\ P_{2} \) . Таким образом, учитывая период косинуса, получим \(\ 120^{\circ}+360^{\circ} \cdot n \leq t \leq 240^{\circ}+360^{\circ} \cdot n \), \(\ n \in Z \)
Сделаем обратную замену \(\ t=2 x+100^{\circ} 120^{\circ}+360^{\circ} \cdot n \leq 2 x+100^{\circ} \leq 240^{\circ}+360^{\circ} \cdot n \), \(\ n \in Z \)
Выразим \(\ \mathbf{x} \), для сначала этого из каждой части неравенства вычтем \(\ 100^{\circ} 120^{\circ}-100^{\circ}+360^{\circ} \cdot n \leq 2 x+100^{\circ}-100^{\circ} \leq 240^{\circ}-100^{\circ}+360^{\circ} \cdot n \), \(\ n \in Z \); \(\ 20^{\circ}+360^{\circ} \cdot n \leq 2 x \leq 140^{\circ}+360^{\circ} \cdot n \), \(\ n \in Z \)
а затем, разделим на 2 \(\ \frac{20^{\circ}+360^{\circ} \cdot n}{2} \leq \frac{2 x}{2} \leq \frac{140^{\circ}+360^{\circ} \cdot n}{2} \), \(\ n \in Z \); \(\ 10^{\circ}+180^{\circ} \cdot n \leq x \leq 70^{\circ}+180^{\circ} \cdot n \), \(\ n \in Z \)
Двойные тригонометрические неравенства
Решить двойное тригонометрическое неравенство \(\ \frac{1}{2}
Введем замену \(\ t=\frac{x}{2} \) , тогда исходное неравенство примет вид \(\ \frac{1}{2}
Решим его, используя единичную окружность. Так как на единичной окружности синусу соответствует ось ординат, выделим на ней множество ординаты которых больше \(\ x=\frac{1}{2} \) и меньше или равно \(\ \frac{\sqrt{2}}{2} \) . На рисунке 8 эти точки будут расположены на дугах \(\ P_{t_{1}} \), \(\ P_{t_{2}} \) и \(\ P_{t_{3}} \), \(\ P_{t_{4}} \) . Найдем значение \(\ t_{1} \), \(\ t_{2} \), \(\ t_{3} \), \(\ t_{4} \) , совершая обход против часовой стрелки, причем \(\ t_{1} \(\ t_{3}=\pi-\arcsin \frac{\sqrt{2}}{2}=\pi-\frac{\pi}{4}=\frac{3 \pi}{4} \); \(\ t_{4}=\pi-\arcsin \frac{1}{2}=\pi-\frac{\pi}{6}=\frac{5 \pi}{6} \)
Таким образом, получаем два интервала, которые, учитывая периодичность функции синус, можно записать следующим образом \(\ \frac{\pi}{6}+2 \pi k \leq t \frac{\pi}{4}+2 \pi k \quad \frac{3 \pi}{4}+2 \pi k Сделаем обратную замену \(\ t=\frac{x}{2} \frac{\pi}{6}+2 \pi k \leq \frac{x}{2} \frac{\pi}{4}+2 \pi k \), \(\ \frac{3 \pi}{4}+2 \pi kВыразим \(\ \mathbf{x} \), для этого умножим все стороны обои неравенств на 2, получим \(\ \frac{\pi}{3}+4 \pi k \leq x
МЕТОДЫ РЕШЕНИЯ ТРИГОНОМЕТРИЧЕСКИХ НЕРАВЕНСТВ
Актуальность. Исторически сложилось, что тригонометрическим уравнениям и неравенствам уделялось особое место в школьном курсе. Можно сказать, что тригонометрия является одним из важнейших разделов школьного курса и всей математической науки в целом.
Тригонометрические уравнения и неравенства занимают одно из центральных мест в курсе математики средней школы, как по содержанию учебного материала, так и по способам учебно-познавательной деятельности, которые могут и должны быть сформированы при их изучении и применены к решению большого числа задач теоретического и прикладного характера.
Решение тригонометрических уравнений и неравенств создаёт предпосылки для систематизации знаний учащихся, связанных со всем учебным материалом по тригонометрии (например, свойства тригонометрических функций, приёмы преобразования тригонометрических выражений и т.д.) и даёт возможность установить действенные связи с изученным материалом по алгебре (уравнения, равносильность уравнений, неравенства, тождественные преобразования алгебраических выражений и т.д.).
Иначе говоря, рассмотрение приёмов решения тригонометрических уравнений и неравенств предполагает своего рода перенос этих умений на новое содержание.
Значимость теории и ее многочисленные применения являются доказательством актуальности выбранной темы. Это в свою очередь позволяет определить цели, задачи и предмет исследования курсовой работы.
Цель исследования: обобщить имеющиеся типы тригонометрических неравенств, основные и специальные методы их решения, подобрать комплекс задач для решения тригонометрических неравенств школьниками.
Задачи исследования:
1. На основе анализа имеющейся литературы по теме исследования систематизировать материал.
2. Привести комплекс заданий, необходимый для закрепления темы «Тригонометрические неравенства».
Объектом исследования являются тригонометрические неравенства в школьном курсе математики.
Предмет исследования: типы тригонометрических неравенств и методы их решения.
Теоретическая значимость заключается в систематизации материала.
Практическая значимость: применение теоретических знаний в решении задач; разбор основных часто встречающихся методов решений тригонометрических неравенств.
Методы исследования : анализ научной литературы, синтез и обобщение полученных знаний, анализ решения заданий, поиск оптимального методов решения неравенств.
§1. Типы тригонометрических неравенств и основные методы их решения
1.1. Простейшие тригонометрические неравенства
Два тригонометрических выражения, соединённые между собой знаком или >, называются тригонометрическими неравенствами.
Решить тригонометрическое неравенство – это значит, найти множество значений неизвестных, входящих в неравенство, при которых неравенство выполняется.
Основная часть тригонометрических неравенств решается сведением их к решению простейших:
Это может быть метод разложения на множители, замены переменного (
, 
и т.д.), где сначала решается обычное неравенство, а затем неравенство вида 
и т.д., или другие способы.
Простейшие неравенства решаются двумя способами: с помощью единичной окружности или графически.
Пусть
f(х
– одна из основных тригонометрических функций. Для решения неравенства 
достаточно найти его решение на одном периоде, т.е. на любом отрезке, длина которого равна периоду функции
f
x
. Тогда решением исходного неравенства будут все найденные
x
, а также те значения, которые отличаются от найденных на любое целое число периодов функции. При этом удобно использовать графический метод.
Приведем пример алгоритма решения неравенств
(
) и
.
Алгоритм решения неравенства
(
).
1. Сформулируйте определение синуса числа x на единичной окружности.
3. На оси ординат отметьте точку с координатой a .
4. Через данную точку проведите прямую, параллельную оси OX, и отметьте точки пересечения ее с окружностью.
5. Выделите дугу окружности, все точки которой имеют ординату, меньшую a .
6. Укажите направление обхода (против часовой стрелки) и запишите ответ, добавив к концам промежутка период функции
2πn
,
.
Алгоритм решения неравенства
.
1. Сформулируйте определение тангенса числа x на единичной окружности.
2. Нарисуйте единичную окружность.
3. Проведите линию тангенсов и на ней отметьте точку с ординатой a .
4. Соедините данную точку с началом координат и отметьте точку пересечения полученного отрезка с единичной окружностью.
5. Выделите дугу окружности, все точки которой имеют на линии тангенсов ординату, меньшую a .
6. Укажите направление обхода и запишите ответ с учетом области определения функции, добавив период
πn
,
(число, стоящее в записи слева, всегда меньше числа, стоящего справа).
Графическая интерпретация решений простейших уравнений и формулы решения неравенств в общем виде указаны в приложении (Приложения 1 и 2).
Пример 1.
Решите неравенство
.
На единичной окружности проводим прямую
, которая пересекает окружность в точках A и B.
Все значения
y
на промежутке NM больше
, все точки дуги AMB удовлетворяют данному неравенству. При всех углах поворота, больших
, но меньших
,
будет принимать значения больше
(но не больше единицы).
Рис.1
Таким образом, решением неравенства будут все значения на интервале
, т.е.
. Для того, чтобы получить все решения данного неравенства, достаточно к концам этого промежутка прибавить
, где
, т.е.
,
.
Заметим, что значения
и
являются корнями уравнения
,
т.е.
;
.
Ответ:
, .
1.2. Графический метод
На практике довольно часто оказывается полезным графический метод решения тригонометрических неравенств. Рассмотрим сущность метода на примере неравенства 
:
1. Если аргумент – сложный (отличен от х ), то заменяем его на t .
2. Строим в одной координатной плоскости
tOy
графики функций 
и 
.
3. Находим такие
две соседние точки пересечения графиков
, между которыми
синусоида
располагается
выше
прямой
. Находим абсциссы этих точек.
4. Записываем двойное неравенство для аргумента t , учитывая период косинуса (t будет между найденными абсциссами).
5. Делаем обратную замену (возвращаемся к первоначальному аргументу) и выражаем значение х из двойного неравенства, записываем ответ в виде числового промежутка.
Пример 2. Решить неравенство: .
При решении неравенств графическим методом необходимо как можно более точно построить графики функций. Преобразуем неравенство к виду:
Построим в одной системе координат графики функций 
и 
(рис. 2).
Рис.2
Графики функций пересекаются в точке
А
с координатами 
; 
. На промежутке 
точки графика 
ниже точек графика 
. А при значения функции совпадают. Поэтому при 
.
Ответ: 
.
1.3. Алгебраический метод
Довольно часто исходное тригонометрическое неравенство путем удачно выбранной подстановки удается свести к алгебраическому (рациональному или иррациональному) неравенству. Данный метод подразумевает преобразование неравенства, введение подстановки или замену переменной.
Рассмотрим на конкретных примерах применение этого метода.
Пример 3.
Приведение к простейшему виду
.
(рис. 3)
Рис.3
, 
.
Ответ: 
,
Пример 4. Решить неравенство:
ОДЗ: 
, 
.
Используя формулы: 
, 
запишем неравенство в виде: 
.
Или, полагая 
после несложных преобразований получим
,
,
.
Решая последнее неравенство методом интервалов, получаем:
Рис.4
, соответственно 
. Тогда из рис. 4 следует 
, где 
.
Рис.5
Ответ:
, 
.
1.4. Метод интервалов
Общая схема решения тригонометрических неравенств методом интервалов:
С помощью тригонометрических формул разложить на множители.
Найти точки разрыва и нули функции, поставить их на окружность.
Взять любую точку К (но не найденную ранее) и выяснить знак произведения. Если произведение положительно, то поставить точку за единичной окружностью на луче, соответствующему углу. Иначе точку поставить внутри окружности.
Если точка встречается четное число раз, назовем ее точкой четной кратности, если нечетное число раз – точкой нечетной кратности. Провести дуги следующим образом: начать с точки К , если следующая точка нечетной кратности, то дуга пересекает окружность в этой точке, если же точка четной кратности, то не пересекает.
Дуги за окружностью – положительные промежутки; внутри окружности – отрицательные промежутки.
Пример 5. Решить неравенство
, 
.
Точки первой серии: 
.
Точки второй серии: 
.
Каждая точка встречается нечетное число раз, то есть все точки нечетной кратности.
Выясним знак произведения при 
: . Отметим все точки на единичной окружности (рис.6):
Рис. 6
Ответ: 
, 
; 
, 
; 
, 
.
Пример 6 . Решите неравенство .
Решение:
Найдём нули выражения .
Получ ae м :
,
;
, 
;
, 
;
, 
;
На единичной окружности значения серии
х
1
представлены точками 
. Серия
х
2
дает точки 
. Из серии
х
3
получаем две точки 
. Наконец, серию
х
4
будут представлять точки 
. Нанесем все эти точки на единичную окружность, указав в скобках рядом с каждой из них ее кратность.
Пусть теперь число 
будет равным. Делаем прикидку по знаку:
Значит, точку
A
следует выбрать на луче, образующем угол 
с лучом
Ох,
вне единичной окружности. (Заметим, что вспомогательный луч
О
A
совсем не обязательно изображать на рисунке. Точка
A
выбирается приблизительно.)
Теперь от точки
A
ведем волнообразную непрерывную линию последовательно ко всем отмеченным точкам. Причем в точках наша линия переходит из одной области в другую: если она находилась вне единичной окружности, то переходит внутрь нее. Подойдя к точке 
, линия возвращается во внутреннюю область, так как кратность этой точки четная. Аналогично в точке 
(с четной кратностью) линию приходится повернуть во внешнюю область. Итак, начертили некую картинку, изображенную на рис. 7. Она помогает выделить на единичной окружности искомые области. Они обозначены знаком « + ».
Рис.7
Окончательный ответ:
Примечание. Если волнообразную линию после обхода ею всех отмеченных на единичной окружности точек не удается вернуть в точку A , не пересекая окружность в «незаконном» месте, то это означает, что в решении допущена ошибка, а именно пропущено нечетное количество корней.
Ответ : .
§2. Комплекс задач по решению тригонометрических неравенств
В процессе формирования у школьников умений решать тригонометрические неравенства, также можно выделить 3 этапа.
1. подготовительный,
2. формирование умений решать простейшие тригонометрические неравенства;
3. введение тригонометрических неравенств других видов.
Цель подготовительного этапа состоит в том, что необходимо сформировать у школьников умение использовать тригонометрический круг или график для решения неравенств, а именно:
Умения решать простейшие неравенства вида
,
, ,
,
с помощью свойств функций синус и косинус;
Умения составлять двойные неравенства для дуг числовой окружности или для дуг графиков функций;
Умения выполнять различные преобразования тригонометрических выражений.
Реализовать этот этап рекомендуется в процессе систематизации знаний школьников о свойствах тригонометрических функций. Основным средством могут служить задания, предлагаемые учащимся и выполняемые либо под руководством учителя, либо самостоятельно, а так же навыки наработанные при решении тригонометрических уравнений.
Приведем примеры таких заданий:
1
. Отметьте на единичной окружности точку
, если
.
2.
В какой четверти координатной плоскости расположена точка
, если
равно:
3.
Отметьте на тригонометрической окружности точки
, если:
4. Приведите выражение к тригонометрическим функциям I четверти.
а)
,
б)
,
в)
5. Дана дуга МР. М – середина I -ой четверти, Р – середина II -ой четверти. Ограничить значение переменной t для: (составить двойное неравенство) а) дуги МР; б) дуги РМ.
6. Записать двойное неравенство для выделенных участков графика:
Рис. 1
7.
Решите неравенства
, 
, 
, 
.
8. Преобразовать выражение .
На втором этапе обучения решению тригонометрических неравенств можно предложить следующие рекомендации, связанные с методикой организации деятельности учащихся. При этом нужно ориентироваться на уже имеющиеся у учащихся умения работать с тригонометрической окружностью или графиком, сформированные во время решения простейших тригонометрических уравнений.
Во-первых, мотивировать целесообразность получения общего приема решения простейших тригонометрических неравенств можно, обратившись, например, к неравенству вида
.
Используя знания и умения, приобретенные на подготовительном этапе, учащиеся приведут предложенное неравенство к виду
, но могут затрудниться в нахождении множества решений полученного неравенства, т.к. только лишь используя свойства функции синус решить его невозможно. Этого затруднения можно избежать, если обратиться к соответствующей иллюстрации (решение уравнения графически или с помощью единичной окружности).
Во-вторых, учитель должен обратить внимание учащихся на различные способы выполнения задания, дать соответствующий образец решения неравенства и графическим способом и с помощью тригонометрического круга.
Рассмотрим такие варианты решения неравенства
.
1. Решение неравенства с помощью единичной окружности.
На первом занятии по решению тригонометрических неравенств предложим учащимся подробный алгоритм решения, который в пошаговом представлении отражает все основные умения, необходимые для решения неравенства.
Шаг 1.
Начертим единичную окружность, отметим на оси ординат точку
и проведем через нее прямую, параллельную оси абсцисс. Эта прямая пересечет единичную окружность в двух точках. Каждая из этих точек изображает числа, синус которых равен
.
Шаг 2.
Эта прямая разделила окружность на две дуги. Выделим ту из них, на которой изображаются числа, имеющие синус больший, чем
. Естественно, эта дуга расположена выше проведенной прямой.
Рис. 2
Шаг 3.
Выберем один из концов отмеченной дуги. Запишем одно из чисел, которое изображается этой точкой единичной окружности
.
Шаг 4.
Для того чтобы выбрать число, соответствующее второму концу выделенной дуги, "пройдем" по этой дуге из названного конца к другому. При этом напомним, что при движении против часовой стрелки числа, которые мы будем проходить, увеличиваются (при движении в противоположном направлении числа уменьшались бы). Запишем число, которое изображается на единичной окружности вторым концом отмеченной дуги
.
Таким образом, мы видим, что неравенству
удовлетворяют числа, для которых справедливо неравенство
. Мы решили неравенство для чисел, расположенных на одном периоде функции синус. Поэтому все решения неравенства могут быть записаны в виде 
Учащимся нужно предложить внимательно рассмотреть рисунок и разобраться, почему все решения неравенства
могут быть записаны в виде
, 
.
Рис. 3
Необходимо обратить внимание учащихся на то, что при решении неравенств для функции косинус, прямую проводим параллельно оси ординат.
Графический способ решения неравенства.
Строим графики
и
, учитывая, что
.
Рис. 4
Затем записываем уравнение
и его решение
, 
, 
, найденное с помощью формул
, 
, 
.
(Придавая
n
значения 0, 1, 2, находим три корня составленного уравнения). Значения
являются тремя последовательными абсциссами точек пересечения графиков
и
. Очевидно, что всегда на интервале
выполняется неравенство
, а на интервале
– неравенство
. Нас интересует первый случай, и тогда добавив к концам этого промежутка число, кратное периоду синуса, получим решение неравенства
в виде:
, .
Рис. 5
Подведём итог. Чтобы решить неравенство
, надо составить соответствующее уравнение и решить его. Из полученной формулы найти корни
и
, и записать ответ неравенства в виде:
, .
В-третьих, факт о множестве корней соответствующего тригонометрического неравенства очень наглядно подтверждается при решении его графическим способом.
Рис. 6
Необходимо продемонстрировать учащимся, что виток, который является решением неравенства, повторяется через один и тот же промежуток, равный периоду тригонометрической функции. Так же можно рассмотреть аналогичную иллюстрацию для графика функции синус.
В-четвертых, целесообразно провести работу по актуализации у учащихся приемов преобразования суммы (разности) тригонометрических функций в произведение, обратить внимание школьников на роль этих приемов при решении тригонометрических неравенств.
Организовать такую работу можно через самостоятельное выполнение учащимися предложенных учителем заданий, среди которых выделим следующие:
В-пятых, от учащихся необходимо требовать обязательной иллюстрации решения каждого простейшего тригонометрического неравенства с помощью графика или тригонометрического круга. Обязательно следует обратить внимание на ее целесообразность, в особенности на применение круга, так как при решении тригонометрических неравенств соответствующая иллюстрация служит очень удобным средством фиксации множества решений данного неравенства
Знакомство учащихся с приемами решения тригонометрических неравенств, не являющихся простейшими, целесообразно осуществлять по следующей схеме: обращение к конкретному тригонометрическому неравенству обращение к соответствующему тригонометрическому уравнению совместный поиск (учитель – учащиеся) приема решения самостоятельный перенос найденного приема на другие неравенства этого же вида.
Чтобы систематизировать знания учащихся о тригонометрии, рекомендуем специально подобрать такие неравенства, решение которых требует различных преобразований, которые могут быть реализованы в процессе его решения, акцентировать внимание учащихся на их особенностях.
В качестве таких продуктивных неравенств можно предложить, например, следующие:
В заключение приведем пример комплекса задач по решению тригонометрических неравенств.
1. Решите неравенства:
2. Решите неравенства: 3. Найдите все решения неравенств: 4. Найдите все решения неравенств:а)
, удовлетворяющие условию 
;
б)
, удовлетворяющие условию 
.
5. Найдите все решения неравенств:
а) ;
б) ;
в) 
;
г) 
;
д) 
.
6. Решите неравенства:
а) ;
б) ;
в) ;
г) 
;
д) ;
е) ;
ж) 
.
7. Решите неравенства:
а)
;
б) ;
в) ;
г) .
8. Решите неравенства:
а) ;
б) ;
в) ;
г) 
;
д) 
;
е) ;
ж) 
;
з) .
Задания 6 и 7 целесообразно предложить ученикам, изучающим математику на повышенном уровне, задание 8 – учащимся классов с углубленным изучением математики.
§3. Специальные методы решения тригонометрических неравенств
Специальные методы решения тригонометрических уравнений – то есть те методы, которые можно использовать только для решения тригонометрических уравнений. Эти методы основаны на использовании свойств тригонометрических функций, а также на использовании различных тригонометрических формул и тождеств.
3.1. Метод секторов
Рассмотрим метод секторов для решения тригонометрических неравенств. Решение неравенств вида 
, где
P
(
x
)
и
Q
(
x
)
– рациональные тригонометрические функции (синусы, косинусы, тангенсы и котангенсы входят в них рационально), аналогично решению рациональных неравенств. Рациональные неравенства удобно решать методом интервалов на числовой оси. Его аналогом при решении рациональных тригонометрических неравенств является метод секторов в тригонометрическом круге, для
sinx
и
cosx
(
) или тригонометрическом полукруге для
tgx
и
ctgx
(
).
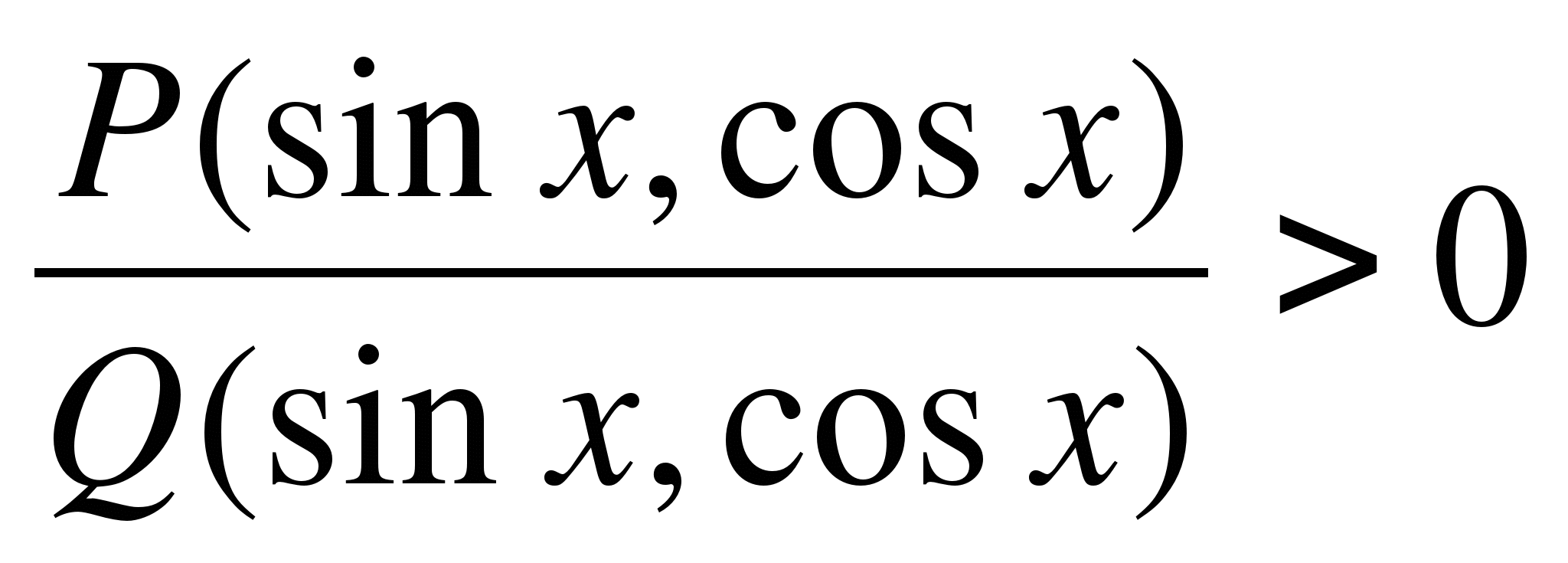
В методе интервалов каждому линейному множителю числителя и знаменателя вида 
на числовой оси соответствует точка 
, и при переходе через эту точку меняет знак. В методе секторов каждому множителю вида 
, где 
- одна из функций
sinx
или
cosx
и 
, в тригонометрическом круге соответствуют два угла 
и 
, которые делят круг на два сектора. При переходе через и функция меняет знак.
Необходимо помнить следующее:
а) Множители вида 
и 
, где 
, сохраняют знак для всех значений 
. Такие множители числителя и знаменателя отбрасывают, изменяя (если 
) при каждом таком отбрасывании знак неравенства на противоположный.
б) Множители вида 
и 
также отбрасываются. При этом, если это множители знаменателя, то в эквивалентную систему неравенств добавляются неравенства вида 
и 
. Если это множители числителя, то в эквивалентной системе ограничений им соответствуют неравенства и в случае строгого исходного неравенства, и равенства 
и 
в случае нестрогого исходного неравенства. При отбрасывании множителя 
или 
знак неравенства изменяется на противоположный.
Пример 1.
Решить неравенства: а) 
, б) 
.
имеем
функция, б) . Решить неравенство Имеем,
3.2. Метод концентрических окружностей
Данный метод является аналогом метода параллельных числовых осей при решении систем рациональных неравенств.
Рассмотрим пример системы неравенств.
Пример 5.
Решить систему простейших тригонометрических неравенств 
Сначала решим каждое неравенство отдельно (рисунок 5). В правом верхнем углу рисунка будем указывать для какого аргумента рассматривается тригонометрическая окружность.
Рис.5
Далее строим систему концентрических окружностей для аргумента х . Рисуем окружность и заштриховываем ее согласно решению первого неравенства, затем рисуем окружность большего радиуса и заштриховываем ее согласно решению второго, далее строим окружность для третьего неравенства и базовую окружность. Из центра системы через концы дуг проводим лучи так, чтобы они пересекали все окружности. На базовой окружности формируем решение (рисунок 6).
Рис.6
Ответ:
, 
.
Заключение
Все задачи курсового исследования были выполнены. Систематизирован теоретический материал: приведены основные типы тригонометрических неравенств и основные методы их решения (графический, алгебраический, метод интервалов, секторов и метод концентрических окружностей). К каждому методы был приведен пример решения неравенства. За теоретической частью следовала практическая. В ней составлен комплекс заданий по решению тригонометрических неравенств.
Данная курсовая может быть использована учащимися для самостоятельной работы. Школьники могут проконтролировать уровень усвоения данной темы, потренироваться в выполнении заданий различной сложности.
Проработав соответствующую литературу по данному вопросу, очевидно, можно сделать вывод о том, что умение и навыки решать тригонометрические неравенства в школьном курсе алгебры и начал анализа являются очень важными, развитие которых требует значительных усилий со стороны учителя математики.
Поэтому данная работа будет полезна учителям математики, так как дает возможность эффективно организовать подготовку учащихся по теме «Тригонометрические неравенства».
Исследование можно продолжить, расширив его до выпускной квалификационной работы .
Список использованной литературы
Богомолов, Н.В. Сборник задач по математике [Текст] / Н.В. Богомолов. – М.: Дрофа, 2009. – 206 с.
Выгодский, М.Я. Справочник по элементарной математике [Текст] / М.Я. Выгодский. – М.: Дрофа, 2006. – 509 с.
Журбенко, Л.Н. Математика в примерах и задачах [Текст] / Л.Н. Журбенко. – М.: Инфра-М, 2009. – 373 с.
Иванов, О.А. Элементарная математика для школьников, студентов и преподавателей [Текст] / О.А. Иванов. – М.: МЦНМО, 2009. – 384 с.
Карп, А.П. Задания по алгебре и началам анализа для организации итогового повторения и проведения аттестации в 11 классе [Текст] / А.П. Карп. – М.: Просвещение, 2005. – 79 с.
Куланин, Е.Д. 3000 конкурсных задач по математике [Текст] / Е.Д. Куланин. – М.: Айрис-пресс, 2007. – 624 с.
Лейбсон, К.Л. Сборник практических заданий по математике [Текст] / К.Л. Лейбсон. – М.: Дрофа, 2010. – 182 с.
Локоть, В.В. Задачи с параметрами и их решение. Тригонометрия: уравнения, неравенства, системы. 10 класс [Текст] / В.В. Локоть. – М.: АРКТИ, 2008. – 64 с.
Манова, А.Н. Математика. Экспресс-репетитор для подготовки к ЕГЭ: уч. пособие [Текст] / А.Н. Манова. – Ростов-на-Дону: Феникс, 2012. – 541 с.
Мордкович, А.Г. Алгебра и начала математического анализа. 10-11 классы. Учебник для учащихся общеобразовательных учреждений [Текст] / А.Г. Мордкович. – М.: Айрис-пресс, 2009. – 201 с.
Новиков, А.И. Тригонометрические функции, уравнения и неравенства [Текст] / А.И. Новиков. – М.: ФИЗМАТЛИТ, 2010. – 260 с.
Оганесян, В.А. Методика преподавания математики в средней школе: Общая методика. Учеб. пособие для студентов физ. - мат. фак. пед. ин-тов. [Текст] / В.А. Оганесян. – М.: Просвещение, 2006. – 368 с.
Олехник, С.Н. Уравнения и неравенства. Нестандартные методы решения [Текст] / С.Н. Олехник. – М.: Изд-во Факториал, 1997. – 219 с.
Севрюков, П.Ф. Тригонометрические, показательные и логарифмические уравнения и неравенства [Текст] / П.Ф. Севрюков. – М.: Народное образование, 2008. – 352 с.
Сергеев, И.Н. ЕГЭ: 1000 задач с ответами и решениями по математике. Все задания группы С [Текст] / И.Н. Сергеев. – М.: Экзамен, 2012. – 301 с.
Соболев, А.Б. Элементарная математика [Текст] / А.Б. Соболев. – Екатеринбург: ГОУ ВПО УГТУ-УПИ, 2005. – 81 с.
Фенько, Л.М. Метод интервалов в решении неравенств и исследовании функций [Текст] / Л.М. Фенько. – М.: Дрофа, 2005. – 124 с.
Фридман, Л.М. Теоретические основы методики обучения математике [Текст] / Л.М. Фридман. – М.: Книжный дом «ЛИБРОКОМ», 2009. – 248 с.
Приложение 1
Графическая интерпретация решений простейших неравенств
Рис. 1
Рис. 2
Рис.3
Рис.4
Рис.5
Рис.6
Рис.7
Рис.8
Приложение 2
Решения простейших неравенств
Проект по алгебре «Решение тригонометрических неравенств» Выполнила ученица 10 «Б» класса Казачкова Юлия Руководитель: учитель математики Кочакова Н.Н.
Цель Закрепить материал по теме «Решение тригонометрических неравенств» и создать памятку ученикам для подготовки к предстоящему экзамену.
Задачи Обобщить материал по данной теме. Систематизировать полученную информацию. Рассмотреть данную тему в ЕГЭ.
Актуальность Актуальность выбранной мною темы заключается в том, что задания на тему «Решение тригонометрических неравенств» входят в задания ЕГЭ.
Тригонометрические неравенства Неравенство - это отношение, связывающее два числа или выражения посредством одного из знаков: (больше); ≥ (больше или равно). Тригонометрическое неравенство – это неравенство, содержащее тригонометрические функции.
Тригонометрические неравенства Решение неравенств, содержащих тригонометрические функции, сводится, как правило, к решению простейших неравенств вида: sin x>a, sin xa, cos x a, tg x a, ctg x
Алгоритм решения тригонометрических неравенств На оси, соответствующей заданной тригонометрической функции, отметить данное числовое значение этой функции. Провести через отмеченную точку прямую, пересекающую единичную окружность. Выделить точки пересечения прямой и окружности с учетом строгого или нестрогого знака неравенства. Выделить дугу окружности, на которой расположены решения неравенства. Определить значения углов в начальной и конечной точках дуги окружности. Записать решение неравенства с учетом периодичности заданной тригонометрической функции.
Формулы решения тригонометрических неравенств sinx >a; x (arcsin a + 2πn; π- arcsin a + 2πn). sinx a; x (- arccos a + 2πn; arccos a + 2πn). cosx a; x (arctg a + πn ; + πn). tgx a; x (πn ; arctg + πn). ctgx
Графическое решение основных тригонометрическх неравенств sinx >a
Графическое решение основных тригонометрическх неравенств sinx Графическое решение основных тригонометрическх неравенств cosx >a Графическое решение основных тригонометрическх неравенств cosx Графическое решение основных тригонометрическх неравенств tgx >a Графическое решение основных тригонометрическх неравенств tgx Графическое решение основных тригонометрическх неравенств ctgx >a
