Derivate parțiale de ordin superior. Derivate parțiale și diferențiale de ordin superior Derivate parțiale de ordin superior

1°

1°. Derivate parțiale de ordin superior. Derivate parțiale de ordinul doi funcțiile z= f(x,y) sunt numite derivate parțiale ale derivatelor sale parțiale de ordinul întâi.

Pentru derivatele de ordinul doi se folosește notația

Derivatele parțiale de ordin mai mare decât secunda sunt definite și notate în mod similar.

Dacă derivatele parțiale care trebuie calculate sunt continue, atunci rezultatul diferențierii repetate nu depinde de ordinea diferențierii.

Exemplu. Găsiți derivatele parțiale de ordinul doi ale funcției.

Soluţie. Să găsim mai întâi derivatele parțiale de ordinul întâi:

Acum facem diferenta a doua oara:

Rețineți că așa-numita derivată parțială „mixtă” poate fi găsită în alt mod și anume: .

2°. Diferențiale de ordin superior. Diferenţial de ordinul doi funcții z=f(x, y) se numește diferenţialul diferenţialului (de ordinul întâi) al acestei funcţii d²z=d(dz).

Diferenţialele unei funcţii r de ordin mai mare decât a doua sunt definite în mod similar, de exemplu: d³z=d(d²z)și în general vorbind, .

Dacă z=f(x,y), Unde Xși y sunt variabile independente, atunci diferența de ordinul 2 a funcției r este calculată prin formula

.

În general, formula simbolică este valabilă

,

care se desfăşoară formal conform legii binomiale.

Dacă z =f(x,y), unde sunt argumentele x și y sunt funcții ale uneia sau mai multor variabile independente, atunci

Dacă x și y sunt variabile independente, d²x =0, d²y =0 și formula (2) devine identică cu formula (1).

Exemplu. Aflați diferențele complete ale ordinului 1 și 2 ale funcției .

A. Vom vorbi din nou doar despre funcțiile a două variabile (dar raționamentul este potrivit și pentru funcții cu orice număr de variabile).

Să avem o funcție

și sunt derivatele sale parțiale. Acestea din urmă, evident, sunt și funcții ale lui x și y și, prin urmare, este posibil să se găsească și derivatele lor parțiale în raport cu x și y.

Derivata parțială în raport cu derivata parțială în raport cu este numită derivată parțială de ordinul doi în raport cu și se notează după cum urmează:

În mod similar definim derivata parțială de ordinul doi în raport cu y:

Derivata parțială în raport cu y a derivatei parțiale în raport cu se numește derivată a doua parțială mixtă în raport cu și în raport cu y:

În mod similar, determinăm derivata a doua parțială, luată mai întâi față de y și apoi față de

Se poate dovedi că pentru multe funcții derivata mixtă nu depinde de ordinea diferențierii, adică că

Nu vom da (din cauza complexității) dovada acestei proprietăți importante, ci o vom demonstra folosind un exemplu.

Fie, de exemplu, să fie dată o funcție

O diferențiem mai întâi în raport cu x și apoi în raport cu

Acum să diferențiem această funcție mai întâi în raport cu y și apoi în raport cu

După cum putem vedea, rezultatul a fost același în ambele cazuri.

Dacă luăm derivate parțiale în raport cu și față de derivatele parțiale de ordinul doi, vom obține derivate parțiale de ordinul al treilea

În mod similar, definim derivate parțiale de ordinul al patrulea, al cincilea etc.

b. La fel cum am luat derivate parțiale ale derivatelor parțiale, putem lua diferența totală a diferenţialului total. Rezultatul se numește a doua diferență totală și este notat în același mod ca a doua diferență a unei funcții a unei variabile, adică astfel:

Al treilea diferenţial total se numeşte diferenţial total al celui de-al doilea diferenţial total etc.

c. Să arătăm acum cum a doua diferență totală este exprimată în termeni de derivate parțiale de ordinul doi. Pentru generalitate, vom presupune că y poate depinde de alte variabile. Să notăm pentru concizie

Pentru a găsi a doua diferență totală, trebuie să luăm prima diferență totală a primei diferențe totale. Reținând în același timp că, așa cum se arată în paragraful „e” al § 3 al acestui capitol, regula de diferențiere a unei sume și a unui produs se aplică și diferenţialului total, putem scrie

Deoarece p și q sunt ele însele funcții ale două variabile x și y, atunci

observa asta

Înlocuindu-le în ultima formulă, după ce deschidem parantezele ajungem în sfârșit

Dacă x și y sunt variabile independente sau funcții liniare ale altor variabile, atunci a doua lor diferență este egală cu zero;

iar formula (8) simplifică:

Vedem că legea invarianței se aplică celei de-a doua diferențe numai cu restricții foarte mari: va fi adevărată numai dacă x și y sunt funcții liniare ale altor variabile, în toate celelalte cazuri nu este aplicabilă. Privind formula (9), vedem că este foarte asemănătoare cu formula pentru pătratul sumei a două numere. Această analogie a dat naștere ideii de a scrie a doua diferență în următoarea formă simbolică:

Despre n, Unde n > 1, din funcție z (\displaystyle z) la un moment dat se numește diferențial în acest punct de diferența de ordine (n - 1), acesta este

re n z = d (d n - 1 z) (\displaystyle d^(n)z=d(d^(n-1)z)) .

YouTube enciclopedic

  • 1 / 5

    Pentru o funcție care depinde de una independent variabilă, a doua și a treia diferență arată astfel:

    d 2 z = d (d z) = d (z ′ d x) = d z ′ d x = (z ″ d x) d x = z ″ d x 2 (\displaystyle d^(2)z=d(dz)=d(z" dx)=dz"dx=(z""dx)dx=z""dx^(2)), d 3 z = d (d 2 z) = d (z ″ d x 2) = d z ″ d x 2 = (z ‴ d x) d x 2 = z ‴ d x 3 (\displaystyle d^(3)z=d(d^) (2)z)=d(z""dx^(2))=dz""dx^(2)=(z"""dx)dx^(2)=z"""dx^(3)).

    De aici putem deriva o viziune generală asupra diferenţialului n ordinea a treia a funcției z = f (x) (\displaystyle z=f(x)), cu conditia ca x (\displaystyle x)- variabila independenta:

    d n z = z (n) d x n (\displaystyle d^(n)z=z^((n))dx^(n)).

    Când se calculează diferențele de ordine superioare, este foarte important ca d x (\displaystyle dx) este arbitrară și independentă de x (\displaystyle x), care, atunci când este diferențiat în raport cu x (\displaystyle x) ar trebui considerat un factor constant. Dacă x (\displaystyle x) nu este o variabilă independentă, atunci diferența va fi diferită (vezi).

    Diferenţială de ordin superior a unei funcţii a mai multor variabile

    Dacă funcţia z = f (x , y) (\displaystyle z=f(x,y)) are derivate parțiale continue de ordinul doi, atunci diferența de ordinul doi este definită după cum urmează: d 2 z = d (d z) (\displaystyle d^(2)z=d(dz)).

    d 2 z = d (∂ z ∂ x d x + ∂ z ∂ y d y) = (∂ z ∂ x d x + ∂ z ∂ y d y) x ′ d x + (∂ z ∂ x d x + ∂ z ∂ redare d y) d^(2)z=d\left((\frac (\partial z)(\partial x))dx+(\frac (\partial z)(\partial y))dy\right)=\left((\) frac (\partial z)(\partial x))dx+(\frac (\partial z)(\partial y))dy\right)"_(x)dx+\left((\frac (\partial z)(\ parțial x))dx+(\frac (\partial z)(\partial y))dy\right)"_(y)dy=) = (∂ 2 z ∂ x 2 d x + ∂ 2 z ∂ y ∂ x d y) d x + (∂ 2 z ∂ x ∂ y d x + ∂ 2 z ∂ y 2 d y) d y (\displaystyle =\left(\frac (\ parțial ^(2)z)(\partial x^(2)))dx+(\frac (\partial ^(2)z)(\partial y\partial x))dy\right)dx+\left((\frac (\partial ^(2)z)(\partial x\partial y))dx+(\frac (\partial ^(2)z)(\partial y^(2)))dy\right)dy) d 2 z = ∂ 2 z ∂ x 2 d x 2 + 2 ∂ 2 z ∂ x ∂ y d x d y + ∂ 2 z ∂ y 2 d y 2 (\displaystyle d^(2)z=(\frac (\partial ^(2)) z)(\partial x^(2)))dx^(2)+2(\frac (\partial ^(2)z)(\partial x\partial y))dxdy+(\frac (\partial ^(2) )z)(\partial y^(2)))dy^(2)) d 2 z = (∂ ∂ x d x + ∂ ∂ y d y) 2 z (\displaystyle d^(2)z=\left((\frac (\partial)(\partial x))dx+(\frac (\partial)( \partial y))dy\right)^(2)z)

    Vedere simbolică generală a diferenţialului n ordinea a treia a funcției z = f (x 1 , . . . , x r) (\displaystyle z=f(x_(1),...,x_(r))) după cum urmează:

    re n z = (∂ ∂ x 1 d x 1 + ∂ ∂ x 2 d x 2 + . . + ∂ ∂ x r d x r) n z (\displaystyle d^(n)z=\left((\frac (\partial )(\partial x_ ( 1)))dx_(1)+(\frac (\partial )(\partial x_(2)))dx_(2)+...+(\frac (\partial )(\partial x_(r)) ) dx_(r)\dreapta)^(n)z)

    Unde z = f (x 1 , x 2 , . . . . x r) (\displaystyle z=f(x_(1),x_(2),...x_(r))), și incremente arbitrare ale variabilelor independente x 1,. . . , x r (\displaystyle x_(1),...,x_(r)).
    Creșteri d x 1,. . . , d x r (\displaystyle dx_(1),...,dx_(r)) sunt considerate constante și rămân aceleași la trecerea de la o diferență la alta. Complexitatea exprimării unui diferențial crește odată cu numărul de variabile.

    Non-invarianța diferenţialelor de ordin superior

    La n ⩾ 2 (\displaystyle n\geqslant 2) n (\displaystyle n) Diferenţialul a treia nu este invariant (spre deosebire de invarianţa primei diferenţiale), adică expresia re n f (\displaystyle d^(n)f) depinde, în general, dacă variabila este luată în considerare x (\displaystyle x) ca una independentă sau ca o funcție intermediară a unei alte variabile, de exemplu, x = φ (t) (\displaystyle x=\varphi (t)).

    Deci, pentru variabila independentă x (\displaystyle x) a doua diferență, așa cum sa menționat mai sus, are forma:

    d 2 z = z ″ (d x) 2 (\displaystyle d^(2)z=z""(dx)^(2))

    Dacă variabila x (\displaystyle x)în sine poate depinde de alte variabile, atunci d (d x) = d 2 x ≠ 0 (\displaystyle d(dx)=d^(2)x\neq 0). În acest caz, formula pentru a doua diferență va arăta astfel:

    d 2 z = d (d z) = d (z ′ d x) = z ″ (d x) 2 + z ′ d 2 x (\displaystyle d^(2)z=d(dz)=d(z"dx)= z""\,(dx)^(2)+z"d^(2)x).

    În mod similar, a treia diferență va lua forma:

    d 3 z = z ‴ (d x) 3 + 3 z ″ d x d 2 x + z ′ d 3 x (\displaystyle d^(3)z=z"""\,(dx)^(3)+3z"" dx\,d^(2)x+z"d^(3)x).

    Pentru a demonstra non-invarianța diferenţialelor de ordin superior, este suficient să dam un exemplu.
    La n = 2 (\displaystyle n=2)Și y = f (x) = x 3 (\displaystyle y=f(x)=x^(3)) :

    Tinand cont de dependenta x = t 2 (\displaystyle x=t^(2)), deja a doua diferență nu are proprietatea de invarianță la schimbarea unei variabile. De asemenea, diferențele de ordine 3 și mai mari nu sunt invariante.

    Suplimente

    • pentru o funcție cu o variabilă:
    4 F (x 0) = d F (x 0) + d 2 F (x 0) 2 ! + . . . + d n F (x 0) n ! + d n + 1 F (x 0 + θ 4 x) (n + 1) ! (\displaystyle (\mathcal (4))F(x_(0))=dF(x_(0))+(\frac (d^(2))F(x_(0)))(2}+...+{\frac {d^{n}F(x_{0})}{n!}}+{\frac {d^{n+1}F(x_{0}+\theta {\mathcal {4}}x)}{(n+1)!}}} !} , (0 < θ < 1) {\displaystyle (0<\theta <1)} ;
    • pentru o funcție cu mai multe variabile:
    4 F (x 0 , y 0) = d F (x 0 , y 0) + d 2 F (x 0 , y 0) 2 ! + . . . + d n F (x 0 , y 0) n ! + d n + 1 F (x 0 + θ 4 x , y 0 + θ 4 y) (n + 1) ! (\displaystyle (\mathcal (4))F(x_(0),y_(0))=dF(x_(0),y_(0))+(\frac (d^(2)F(x_(0)) ),y_(0)))(2}+...+{\frac {d^{n}F(x_{0},y_{0})}{n!}}+{\frac {d^{n+1}F(x_{0}+\theta {\mathcal {4}}x,y_{0}+\theta {\mathcal {4}}y)}{(n+1)!}}} !} , (0 < θ < 1) {\displaystyle (0<\theta <1)}

    Să fie dată o funcție a două variabile. Să dăm argumentului un increment și să lăsăm argumentul neschimbat. Apoi funcția va primi un increment, care se numește increment parțial cu variabilă și se notează:

    În mod similar, fixând argumentul și dând un increment argumentului, obținem o creștere parțială a funcției după variabilă:

    Mărimea se numește increment total al funcției într-un punct.

    Definiție 4. Derivata parțială a unei funcții a două variabile față de una dintre aceste variabile este limita raportului dintre incrementul parțial corespunzător al funcției și incrementul unei variabile date atunci când aceasta din urmă tinde spre zero (dacă această limită există). Derivata parțială se notează după cum urmează: sau, sau.

    Astfel, prin definiție avem:

    Derivatele parțiale ale funcțiilor se calculează după aceleași reguli și formule ca în funcție de o variabilă, ținând cont de faptul că la diferențierea față de o variabilă, aceasta este considerată constantă, iar la diferențierea față de o variabilă, este considerată constantă. .

    Exemplul 3. Găsiți derivate parțiale ale funcțiilor:

    Soluţie. a) Pentru a găsi, o considerăm o valoare constantă și o diferențiem în funcție de o variabilă:

    În mod similar, presupunând o valoare constantă, găsim:

    Definiţie 5. Diferenţialul total al unei funcţii este suma produselor derivatelor parţiale ale acestei funcţii şi a incrementelor variabilelor independente corespunzătoare, i.e.

    Având în vedere că diferențele variabilelor independente coincid cu incrementele acestora, i.e. , formula diferenţialului total poate fi scrisă ca

    Exemplul 4. Aflați diferența completă a funcției.

    Soluţie. Deoarece, folosind formula diferenţială totală găsim

    Derivate parțiale de ordin superior

    Derivatele parțiale sunt numite derivate parțiale de ordinul întâi sau derivate parțiale de primă ordine.

    Definiție 6. Derivatele parțiale de ordinul doi ale unei funcții sunt derivatele parțiale ale derivatelor parțiale de ordinul întâi.

    Există patru derivate parțiale de ordinul doi. Acestea sunt desemnate după cum urmează:

    Derivatele parțiale ale ordinului 3, 4 și superior sunt definite în mod similar. De exemplu, pentru o funcție avem:

    Derivatele parțiale de ordinul doi sau mai mari, luate în raport cu diferite variabile, se numesc derivate parțiale mixte. Pentru o funcție, acestea sunt derivate. Rețineți că în cazul în care derivatele mixte sunt continue, atunci egalitatea este valabilă.

    Exemplul 5. Găsiți derivate parțiale de ordinul doi ale unei funcții

    Soluţie. Derivatele parțiale de ordinul întâi pentru această funcție se găsesc în Exemplul 3:

    Diferențiând față de variabilele x și y, obținem

    Fiecare derivată parțială (prin Xși prin y) a unei funcții a două variabile este derivata obișnuită a unei funcții a unei variabile pentru o valoare fixă ​​a celeilalte variabile:

    (Unde y= const),

    (Unde X= const).

    Prin urmare, derivatele parțiale sunt calculate folosind formule și reguli pentru calcularea derivatelor funcțiilor unei variabile, luând în considerare cealaltă constantă variabilă.

    Dacă nu aveți nevoie de o analiză a exemplelor și de teoria minimă necesară pentru aceasta, ci aveți nevoie doar de o soluție la problema dvs., atunci accesați calculator de derivate parțiale online .

    Dacă este greu să vă concentrați pentru a urmări unde se află constanta în funcție, atunci în schița de soluție a exemplului, în loc de o variabilă cu o valoare fixă, puteți înlocui orice număr - atunci puteți calcula rapid derivata parțială ca derivata obisnuita a unei functii a unei variabile. Trebuie doar să vă amintiți să returnați constanta (o variabilă cu o valoare fixă) la locul ei când terminați proiectul final.

    Proprietatea derivatelor parțiale descrisă mai sus rezultă din definiția derivatelor parțiale, care poate apărea în întrebările de examen. Prin urmare, pentru a vă familiariza cu definiția de mai jos, puteți deschide referința teoretică.

    Conceptul de continuitate a funcției z= f(X, y) într-un punct este definit în mod similar cu acest concept pentru o funcție a unei variabile.

    Funcţie z = f(X, y) se numeste continuu intr-un punct daca

    Diferența (2) se numește increment total al funcției z(se obține ca urmare a creșterii ambelor argumente).

    Să fie dată funcția z= f(X, y) și punct

    Dacă funcția se schimbă z apare atunci când doar unul dintre argumente se schimbă, de exemplu, X, cu o valoare fixă ​​a altui argument y, atunci funcția va primi un increment

    numită creștere parțială a funcției f(X, y) De X.

    Luând în considerare o schimbare a funcției zîn funcție de schimbarea doar a unuia dintre argumente, trecem efectiv la o funcție a unei variabile.

    Dacă există o limită finită

    atunci se numește derivată parțială a funcției f(X, y) prin argumentare Xși este indicată de unul dintre simboluri

    (4)

    Creșterea parțială este determinată în mod similar z De y:

    și derivată parțială f(X, y) De y:

    (6)

    Exemplul 1.

    Soluţie. Găsim derivata parțială față de variabila „x”:

    (y fix);

    Găsim derivata parțială față de variabila „y”:

    (X fix).

    După cum puteți vedea, nu contează în ce măsură variabila este fixă: în acest caz este pur și simplu un anumit număr care este un factor (ca și în cazul derivatei obișnuite) al variabilei cu care găsim derivata parțială. . Dacă variabila fixă ​​nu este înmulțită cu variabila cu care găsim derivata parțială, atunci această constantă singură, indiferent în ce măsură, ca în cazul derivatei obișnuite, dispare.

    Exemplul 2. Dată o funcție

    Găsiți derivate parțiale

    (prin X) și (prin Y) și calculați valorile lor la punctul A (1; 2).

    Soluţie. La fix y derivata primului termen se găsește ca derivată a funcției putere ( tabelul funcțiilor derivate ale unei variabile):

    .

    La fix X derivata primului termen se găsește ca derivată a funcției exponențiale, iar al doilea - ca derivată a unei constante:

    Acum să calculăm valorile acestor derivate parțiale la punctul respectiv A (1; 2):

    Puteți verifica soluția problemelor derivate parțiale la calculator de derivate parțiale online .

    Exemplul 3. Găsiți derivate parțiale ale unei funcții

    Soluţie. Într-un singur pas găsim

    (y X, de parcă argumentul sinelui ar fi 5 X: la fel, 5 apare înaintea semnului funcției);

    (X este fix și este în acest caz un multiplicator la y).

    Puteți verifica soluția problemelor derivate parțiale la calculator de derivate parțiale online .

    Derivatele parțiale ale unei funcții de trei sau mai multe variabile sunt definite în mod similar.

    Dacă fiecare set de valori ( X; y; ...; t) variabile independente din mulţime D corespunde unei anumite valori u din multi E, Acea u numită funcţie de variabile X, y, ..., t si denota u= f(X, y, ..., t).

    Pentru funcțiile a trei sau mai multe variabile, nu există o interpretare geometrică.

    Derivatele parțiale ale unei funcții a mai multor variabile sunt de asemenea determinate și calculate în ipoteza că doar una dintre variabilele independente se modifică, în timp ce celelalte sunt fixe.

    Exemplul 4. Găsiți derivate parțiale ale unei funcții

    .

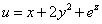    Soluţie. yȘi z fix:

    XȘi z fix:

    XȘi y fix:

    Găsiți singur derivate parțiale și apoi uitați-vă la soluții

    Exemplul 5.

    Exemplul 6. Găsiți derivate parțiale ale unei funcții.

    Derivata parțială a unei funcții a mai multor variabile are același lucru sensul mecanic este același cu derivata unei funcții a unei variabile, este rata de modificare a funcției în raport cu o modificare a unuia dintre argumente.

    Exemplul 8. Valoarea cantitativă a debitului P călătorii feroviari pot fi exprimați prin funcție

    Unde P– numărul de pasageri, N– numărul de rezidenți ai punctelor corespondente, R- distanta dintre puncte.

    Derivată parțială a unei funcții P De R, egal

    arată că scăderea fluxului de pasageri este invers proporțională cu pătratul distanței dintre punctele corespunzătoare cu același număr de rezidenți în puncte.

    Derivată parțială P De N, egal

    arată că creșterea fluxului de pasageri este proporțională cu dublul numărului de locuitori ai localităților aflate la aceeași distanță între puncte.

    Puteți verifica soluția problemelor derivate parțiale la calculator de derivate parțiale online .

    Diferenţial complet

    Produsul unei derivate parțiale și incrementul variabilei independente corespunzătoare se numește diferențială parțială. Diferențele parțiale se notează după cum urmează:

    Suma diferenţialelor parţiale pentru toate variabilele independente dă diferenţialul total. Pentru o funcție a două variabile independente, diferența totală este exprimată prin egalitate

    (7)

    Exemplul 9. Găsiți diferența completă a unei funcții

    Soluţie. Rezultatul utilizării formulei (7):

    Se spune că o funcție care are o diferență totală în fiecare punct al unui anumit domeniu este diferențiabilă în acel domeniu.

    Găsiți singur diferența totală și apoi uitați-vă la soluție

    La fel ca în cazul unei funcții a unei variabile, diferențiabilitatea unei funcții într-un anumit domeniu implică continuitatea acesteia în acest domeniu, dar nu invers.

    Să formulăm fără dovezi o condiție suficientă pentru derivabilitatea unei funcții.

    Teorema. Dacă funcţia z= f(X, y) are derivate parțiale continue

    într-o regiune dată, atunci este diferențiabilă în această regiune și diferența sa este exprimată prin formula (7).

    Se poate arăta că, la fel ca în cazul unei funcții a unei variabile, diferența funcției este principala parte liniară a incrementului funcției, deci în cazul unei funcții de mai multe variabile, diferența totală este principala, liniară în raport cu incrementele variabilelor independente, parte din incrementul total al funcției.

    Pentru o funcție de două variabile, incrementul total al funcției are forma

    (8)

    unde α și β sunt infinitezimale la și .

    Derivate parțiale de ordin superior

    Derivate parțiale și funcții f(X, y) în sine sunt unele funcții ale acelorași variabile și, la rândul lor, pot avea derivate față de diferite variabile, care sunt numite derivate parțiale de ordin superior.